1. Overview
Measures of statistical uncertainty for the local authority mid-year population estimates (MYEs) are research statistics that aim to give users of Office for National Statistics (ONS) data information about their quality. Uncertainty measures for 2012 to 2016 mid-year population estimates were published in 2017. These were produced for each of the 348 local authorities in England and Wales.
In this article, we extend the data time series from 2012 to 2016 to 2011 to 2019. We also incorporate some recent changes made to the mid-year estimate methodology (see Population estimates for local authorities in England and Wales new methods) into the uncertainty measures approach.
We use the cohort component method to create the local authority MYEs. This method uses the 2011 Census for the population base and then incorporates natural change (births and deaths), net international migration and net internal migration, and other adjustments (for example, asylum seekers). The census, international and internal migration are the main sources of uncertainty in the MYEs.
The uncertainty methodology assumes that there is zero error in the other components such as births and deaths. Since the MYEs combine various data sources and processes to derive each component, we have used tailored methods to produce 1,000 simulated values for each component. These are then combined using the cohort component formula to derive the uncertainty associated with the local authority MYEs. The methods for producing uncertainty measures at local authority level are described in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016.
In the previous article we provided three types of uncertainty intervals: bias-adjusted, empirical and centred empirical. We also noted that the bias-adjusted was our preferred method as it produced wider intervals and was more conservative. However, these intervals also become less reliable as we approach the 2021 Census when uncertainty around the mid-year estimates is at its highest level.
For this reason, in this article we favour the empirical 95% uncertainty intervals. We also provide nearest 95% uncertainty intervals. We provide both in the Measures of uncertainty – all confidence intervals dataset to support understanding of our methodological approach and of the options available.
We interpret the uncertainty intervals in the following way. If the assumptions we have made in estimating uncertainty are correct, we would expect these intervals on average to capture the true population 95% of the time.
In addition to the uncertainty measures, we also show in the Measures of uncertainty with proportional contributions dataset the proportion of the uncertainty that is attributable to each of the three components: the census, international migration and internal migration.
Nôl i'r tabl cynnwys2. Methodology
Local authority mid-year population estimates (MYEs) are calculated using the cohort component method. In this approach, the previous year's population is aged-on by one year and then adjusted for births, deaths, net international migration, net internal migration and special populations (such as members of the armed forces and prisoners). The data for these adjustments come from several sources:
- data on births and deaths come from the General Register Office administrative registers
- national-level international immigration estimates come from the International Passenger Survey (IPS) and are distributed to local authority level using census and administrative data sources
- regional level international emigration estimates come from the IPS and are distributed to local authority level using a Poisson regression model incorporating census, survey and administrative data
- data on asylum seekers and their dependants come from the Immigration and Nationality Directorate of the Home Office
- internal migration data are primarily based on the NHS Patient Register
- adjustments are also made for special population sub-groups that are not captured in the international and internal migration estimates, for example, members of the armed forces and prisoners
The estimation process is repeated each year, starting from the 2011 Census base and rolled forward using the cohort component method. Uncertainty from international and internal migration includes accumulated uncertainty from previous years rolled forward, plus new uncertainty for the given year. This means that the uncertainty accumulates over time. The longer the lapse since the census, the more uncertainty there will be in the estimates.
“Uncertainty” is defined here as the quantification of doubt about a measurement. The three main sources of uncertainty associated with the MYEs are the census base, international migration and internal migration (moves between local authorities). Uncertainty in the other components of change (births, deaths, asylum seekers, armed forces and prisoners) is not reflected in the methodology and is assumed to be zero.
We estimate uncertainty using statistical bootstrapping methods (PDF, 15.3MB) (Efron and Tibshirani, 1993). For each of the three components associated with uncertainty, the estimation process that is used to produce the MYEs is replicated and the replicates are used to simulate a range of possible values that might occur. The simulated distributions for each component are combined, iteration by iteration, mirroring the standard cohort components approach that is used for the published MYEs. The uncertainty generation process is summarised in Figure 1.
Figure 1: The mid-year estimate cohort component method and statistical uncertainty
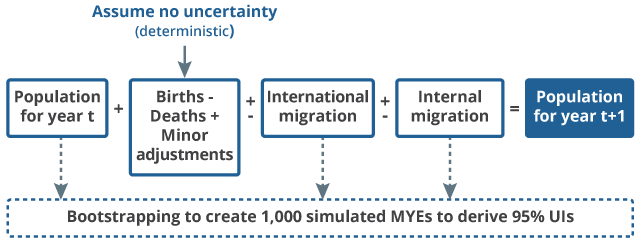
Source: Office for National Statistics
Download this image Figure 1: The mid-year estimate cohort component method and statistical uncertainty
.png (16.6 kB)Empirical 95% uncertainty intervals for each local authority are created by ranking the 1,000 simulated values (from smallest to largest) and taking the 26th and 975th values as the lower and upper bounds respectively. As the observed MYE generally differs from the centre or median of the simulations, this uncertainty interval is not centred around the MYE and in some extreme cases the MYE is outside the uncertainty bounds.
For nearest 95% uncertainty intervals we rank the 1,000 simulated values by their distance (absolute difference) from the MYE. The range of the nearest 950 values provide the uncertainty bounds. This uncertainty interval is more centred around the MYE and usually wider than the empirical uncertainty interval.
Further details on the methods used to measure uncertainty in the MYEs are available in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016.
In this article, we extend the data time series from 2012 to 2016 to 2011 to 2019 and incorporate some recent changes made to the mid-year estimate methodology (see Population estimates for local authorities in England and Wales new methods) into the uncertainty measures approach, as described in this section.
For emigrants, prior to 2017 the population estimates were produced by taking a multi-stage approach:
- The IPS data were averaged across three years: the current year and the two preceding years.
- The averages were constrained to the New Migration Geography outflow (NMGo) level.
- The counts were distributed down to local authority (LA) level using a fixed Poisson regression model. The model uses LA level census, administrative and survey data as covariates to model international emigration at LA level.
From 2017 onwards, this was simplified to a two-stage approach, after removing the NMGo geographies, as their use was not in line with international best practice. Under the new approach:
- The IPS data were averaged across three years: the current year and the two preceding years.
- The counts were distributed down to LA level using a fixed Poisson regression model. The model uses LA level census, administrative and survey data as covariates to model international emigration at LA level. The number and nature of the covariates changed from the previous method. The regression model also now applies an offset term (population size from the preceding year), which is the preferred option in the demographic literature. This moves from modelling counts of flows to modelling emigration rates.
4. Location of the MYEs in their uncertainty intervals
Tables 3 and 4 show that for most local authorities, the mid-year population estimate (MYE) sits within its uncertainty interval for every year, for both empirical and nearest 95% intervals.
Over time, a growing number of local authority MYEs fall outside of their empirical 95% uncertainty bounds (Table 3). By 2019, nearly half of local authority mid-year estimates do. This is consistent with our understanding that estimation of the population becomes progressively more difficult as we move away from the census. The nearest 95% uncertainty intervals are closer to the mid-year estimates and by 2019 only a quarter of local authority MYEs fall outside of the uncertainty bounds (Table 4).
| Year | Number within | % | Number above | % | Number below | % |
|---|---|---|---|---|---|---|
| 2011 | 348 | 100.00 | ||||
| 2012 | 347 | 99.71 | 1 | 0.29 | ||
| 2013 | 316 | 90.80 | 28 | 8.05 | 4 | 1.15 |
| 2014 | 271 | 77.87 | 66 | 18.97 | 11 | 3.16 |
| 2015 | 237 | 68.10 | 95 | 27.30 | 16 | 4.60 |
| 2016 | 218 | 62.64 | 108 | 31.03 | 22 | 6.32 |
| 2017 | 195 | 56.03 | 120 | 34.48 | 33 | 9.48 |
| 2018 | 187 | 53.74 | 123 | 35.34 | 38 | 10.92 |
| 2019 | 177 | 50.86 | 130 | 37.36 | 41 | 11.78 |
Download this table Table 3: Position of local authority mid-year population estimates relative to their empirical 95% uncertainty intervals, 2011 to 2019
.xls .csv
| Year | Number within | % | Number above | % | Number below | % |
|---|---|---|---|---|---|---|
| 2011 | 348 | 100.00 | ||||
| 2012 | 348 | 100.00 | ||||
| 2013 | 346 | 99.43 | 1 | 0.29 | 1 | 0.29 |
| 2014 | 335 | 96.26 | 10 | 2.87 | 3 | 0.86 |
| 2015 | 311 | 89.37 | 30 | 8.62 | 7 | 2.01 |
| 2016 | 300 | 86.21 | 38 | 10.92 | 10 | 2.87 |
| 2017 | 282 | 81.03 | 50 | 14.37 | 16 | 4.60 |
| 2018 | 272 | 78.16 | 59 | 16.95 | 17 | 4.89 |
| 2019 | 262 | 75.29 | 65 | 18.68 | 21 | 6.03 |
Download this table Table 4: Position of local authority mid-year population estimates relative to their nearest 95% uncertainty intervals, 2011 to 2019
.xls .csvTable 5 shows that for 87 local authorities the MYE sits comfortably within its empirical 95% uncertainty interval across the whole time period. For the nearest 95% interval, this is 169. By 2019, 121 MYEs cross the upper bound of their empirical uncertainty interval, compared with 56 for the nearest 95% uncertainty interval.
| Position over time | Empirical 95% | Nearest 95% |
|---|---|---|
| MYE sits within the uncertainty interval | 87 | 169 |
| MYE drifts to upper bound | 58 | 62 |
| MYE drifts to lower bound | 38 | 35 |
| MYE crosses upper bound | 121 | 56 |
| MYE crosses lower bound | 39 | 18 |
| MYE follows none of these trends | 5 | 8 |
| Total | 348 | 348 |
Download this table Table 5: Position of local authority mid-year population estimates relative to their uncertainty intervals, 2011 to 2019
.xls .csvFigures 2 to 7 provide illustrative examples of local authorities of each of the types listed in Table 5.
Figure 2: The mid-year population estimate sits within its uncertainty intervals – Boston
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 2: The mid-year population estimate sits within its uncertainty intervals – Boston
Image .csv .xls
Figure 3: The mid-year population estimate drifts to the upper bound of the uncertainty intervals – County Durham
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 3: The mid-year population estimate drifts to the upper bound of the uncertainty intervals – County Durham
Image .csv .xls
Figure 4: The mid-year population estimate drifts to the lower bound of the uncertainty intervals – Cardiff
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 4: The mid-year population estimate drifts to the lower bound of the uncertainty intervals – Cardiff
Image .csv .xls
Figure 5: The mid-year estimate crosses the upper bound of the uncertainty intervals – Mid Devon
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 5: The mid-year estimate crosses the upper bound of the uncertainty intervals – Mid Devon
Image .csv .xls
Figure 6: The mid-year population estimate crosses the lower bound of the uncertainty intervals – Cheltenham
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 6: The mid-year population estimate crosses the lower bound of the uncertainty intervals – Cheltenham
Image .csv .xls
Figure 7: The mid-year population estimate follows none of the trends above – Wandsworth
Source: Office for National Statistics - measures of statistical uncertainty
Download this chart Figure 7: The mid-year population estimate follows none of the trends above – Wandsworth
Image .csv .xls5. Summary and limitations
Our local authority mid-year population estimates (MYEs) are the best estimates of the usually resident population that are currently available between the decennial census years. The processes used to derive the mid-year estimates are complex, with many different components. Some uncertainty around them is, therefore, expected.
The complexity of the methodology makes it impossible to estimate this uncertainty directly. The methodology described in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016 quantifies uncertainty and indicates the relative contribution to this uncertainty by each of the three components that impact on uncertainty the most: the 2011 Census base, international and internal migration.
Uncertainty measures derived using this methodology were published in 2017 for the data time series 2012 to 2016. These were produced for each of the 348 local authorities in England and Wales. This article presents the extension of the time series to 2011 to 2019 and the incorporation of recent changes made to the MYE methodology into the uncertainty measures approach. We provide two uncertainty intervals, empirical and nearest 95%.
The uncertainty methodology is based on three components with the greatest impact on uncertainty. The measures do not incorporate the uncertainty associated with all of the data sources and processes involved in producing MYEs and should be considered to be conservative.
Bias in the mid-year estimates, represented by the difference between the median of the simulated populations for each year and the corresponding published MYE, is primarily attributable to the discrepancy between our modelled post-census internal migration flows and the corresponding flows in the published MYEs.
Our uncertainty methods assume that the relationship between internal migration taken from the census and from the Patient Register (supplemented by the Higher Education Statistics Agency) remains constant over time, given the covariates. Increasingly we suspect that this does not hold, given recent initiatives within the NHS to clean their Patient Registers. List-cleaning activity is geographically uneven and will generate anomalous simulated internal migration flows.
The proportional contributions to uncertainty from the 2011 Census, internal and international migration follow expected patterns. The relative influence of the 2011 Census on uncertainty declines over time, as the estimates for areas with high population churn are more heavily influenced by the internal and international migration components.
Every care has been taken to implement and quality assure the methodology and outputs. However, this approach depends on the assumptions made when constructing them and the input data used to generate the outputs. Sometimes, the method generates extreme values that would be unlikely to arise in reality. This does not undermine our confidence in the methodology or the data, rather it emphasises the need for caution in interpreting these results.
We welcome comments and observations on these research methods and results. This project has involved applying statistical bootstrapping in a range of contexts and on a range of data sources. As we increasingly move towards statistics that integrate survey, administrative and other sources, the relevance of these approaches is becoming more apparent.
Acknowledgements
Professor Peter Smith from the University of Southampton Statistical Sciences Research Institute has helped us to develop the measures of statistical uncertainty described in this article. We are also indebted to him for his comments and suggestions in the research and writing of this article.
Nôl i'r tabl cynnwys