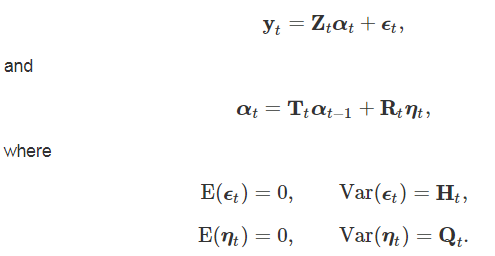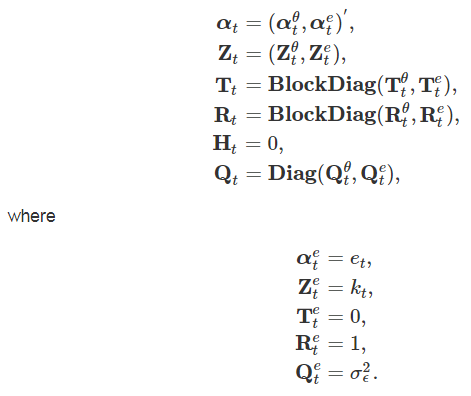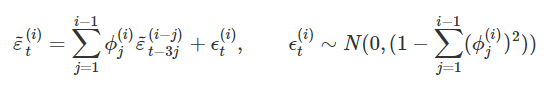1. Main points
Experimental single-month estimates for the number of people in employment, unemployment and inactivity, for ages 16 years and over, and ages 16 to 64 years have been produced using time series models.
The input data for the models are single-month wave-specific time series estimates for each variable and their estimated variances.
The time series models assume that each observed time series comprises an underlying population process (the “true” number of people employed, unemployed or inactive, that are each modelled as having an underlying level and seasonality that can vary over time) and a wave-specific survey error.
The published “levels” for each series are seasonally adjusted model-based estimates; these are the estimated population process minus the estimated seasonal component for that series (which has also been estimated as part of the model).
2. Introduction
New experimental single-month estimates for the main Labour Force Survey (LFS) variables have been developed using time series models to estimate the level of employed, unemployed and inactive for ages 16 years and over, and ages 16 to 64 years.
Single-month estimates using standard calibration weighting are volatile. The time series model estimates and removes what is assumed to be sampling error to provide estimates of the unobserved level of each variable.
This article explains the methods used for estimation of these experimental LFS estimates. The main text provides a more accessible description of the models using unemployment for ages 16 years and over as an example. This covers a description of how the input data for the models are derived, the structure of the models and the main outputs. A technical section on the model specification can be found in the Appendix.
Nôl i'r tabl cynnwys3. Model inputs
Five different wave-specific estimates of unemployment for those aged 16 years and over are estimated from the survey data. Wave-specific simply means that the estimates are based only on respondents who are in the same wave.
A wave indicates how many times a respondent has been sampled (the survey design of the Labour Force Survey (LFS) means that respondents, once selected, are included five times at 13-week intervals). As can be seen in Figure 1, the estimates are quite volatile.
Figure 1: Single-month wave-specific estimates for UK unemployment ages 16 years and over
January 2002 to February 2019
Source: Office for National Statistics - Labour Force Survey
Download this chart Figure 1: Single-month wave-specific estimates for UK unemployment ages 16 years and over
Image .csv .xlsThe monthly wave-specific time series are estimated using a simplified version of the calibration weighting described in Office for National Statistics (2016). Simplified calibration groups are required because once a quarterly period has been separated into three monthly periods and five waves the sample size is significantly reduced for each group.
As with the estimation for the rolling-quarterly data, there is no adjustment to the weights for non-reponse and attrition other than the adjustments from calibration. The simplified calibration groups include aggregating up some of the geographical classifications as well as some age classifications; sex is also used for constructing the calibration groups.
Wave-specific estimates have been estimated from January 2002 onwards, because of the ease of access of the sample data. The wave-specific estimates can be averaged to provide one single-month time series. Note that the averaged monthly wave-specific estimates differ slightly to the currently published single-month estimates, as the method of estimation differs. Information on the current methods for single-month estimates can be found in Office for National Statistics (2019).
The sample at any time period less than three months is clustered. The variance estimation for the single-month wave-specific estimates is done using the linearised jackknife estimator of Skinner and Holmes (2000) accounting for the clustering, stratification and calibration.
Nôl i'r tabl cynnwys4. Model structure
In time series modelling, a commonly-assumed structure for many official statistics is that a time series comprises a number of unobserved components such as a trend (underlying level), a seasonal component and an irregular component.
The time series model used for these experimental estimates assumes a number of unobserved components exist for each monthly wave-specific time series. These include a population process (the “true” level of unemployment) that is common to all of the observed time series and an error term that is specific to each wave.
The population process itself comprises a trend and seasonal component. The wave-specific error terms include a wave-specific bias (as the average level for each wave-specific time series may systematically differ) and a wave-specific sampling error.
There is sample overlap at a three-month lag (13 weeks, note that Labour Force Survey (LFS) months are four or five weeks in length), which means that wave 2 respondents at month t were in wave 1 at t −3, wave 3 respondents at month t were in wave 2 at t −3 and wave 1 at t −6 and so on. The sample overlap causes correlation in the sampling error between wave-specific estimates, which is useful to help model the sampling error. This correlation is estimated using what is termed a pseudo-survey error autocorrelation approach (see Pfeffermann, Feder, and Signorelli (1998)).
Estimates of the correlation for unemployment for ages 16 years and over are given in Table 1.
Table 1: Pseudo-survey error autocorrelation estimates of the cross-correlation between the indicated wave i and wave i-l at lag t-3 l
| Wave 2 | Wave 3 | Wave 4 | Wave 5 | |
|---|---|---|---|---|
| t – 3 | 0.593 | 0.549 | 0.502 | 0.651 |
| t – 6 | 0.439 | 0.183 | 0.300 | |
| t – 9 | 0.246 | 0.112 | ||
| t – 12 | 0.201 |
The design-based standard errors of the monthly wave-specific estimates are also used as input data in the model to account for any changing variance over time. The design-based standard errors are as shown in Figure 2.
Figure 2: Single-month wave-specific design-based estimates of standard errors for UK unemployment ages 16 years and over
January 2002 to February 2019
Source: Office for National Statistics - Labour Force Survey
Download this chart Figure 2: Single-month wave-specific design-based estimates of standard errors for UK unemployment ages 16 years and over
Image .csv .xlsIt is possible to write equations to describe the population process and wave-specific error processes, and all of these can be put into the state-space framework.
The state-space model is formed of two equations, the observation and the transition equation. The observation equation describes how the monthly wave-specific estimates (the observed data) relate to the unobserved components in the model. The unobserved components are in the state vector ( αt ). The transition equation describes how the unobserved components in the state vector evolve over time.
Once the model has been specified, there are certain parameters that require estimation. Coefficients for the correlation of the sampling errors are derived from the pseudo-survey error autocorrelation approach, and variances and any co-variances for the error terms in the model (also known as hyper-parameters) are estimated using maximum likelihood. Finally, the unobserved components in the model can be estimated using the Kalman filter and Kalman smoother.
Nôl i'r tabl cynnwys5. Model outputs
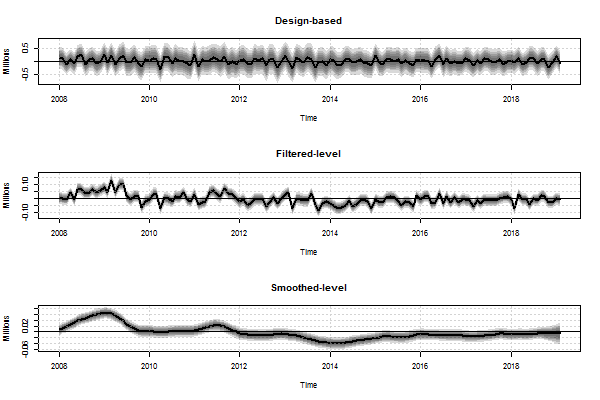
The state-space model produces, among other things, filtered estimates of each of the unobserved components, that is to say the best estimate of each component at time point t using only observed data up to time point t for the estimation. Smoothed estimates of each of the unobserved components at time point t can be computed using all available data.
Figure 3 plots the filtered and smoothed estimates of the level of monthly UK unemployment for ages 16 years and over. If hyper-parameters are not re-estimated then when additional time points are available the smoothed estimates will be revised, but the filtered estimates are not revised.
Figure 3: Single-month wave-specific estimates and filtered and smoothed estimates of the level of UK unemployment ages 16 years and over
January 2004 to February 2019
Source: Office for National Statistics - Labour Force Survey
Download this chart Figure 3: Single-month wave-specific estimates and filtered and smoothed estimates of the level of UK unemployment ages 16 years and over
Image .csv .xlsPlots of the estimated seasonal component and also the wave-specific bias components for UK unemployment for those aged 16 years and over are shown in Figure 4. As can be seen, seasonality is not strong in the series, although it is found to be statistically significant. Similarly the wave-specific biases are relatively small in magnitude but are also found to be statistically significant.
Figure 4: Smoothed estimates of seasonal and wave-specific bias components for UK unemployment ages 16 years and over
January 2004 to February 2019

Source: Office for National Statistics - Labour Force Survey
Download this image Figure 4: Smoothed estimates of seasonal and wave-specific bias components for UK unemployment ages 16 years and over
.png (5.6 kB) .xlsx (27.1 kB)In contrast to the seasonal and wave-specific bias terms, the estimated wave-specific sampling errors are relatively large, as can be seen in Figure 5.
Figure 5: Smoothed estimates of wave-specific sampling error for UK unemployment ages 16 years and over
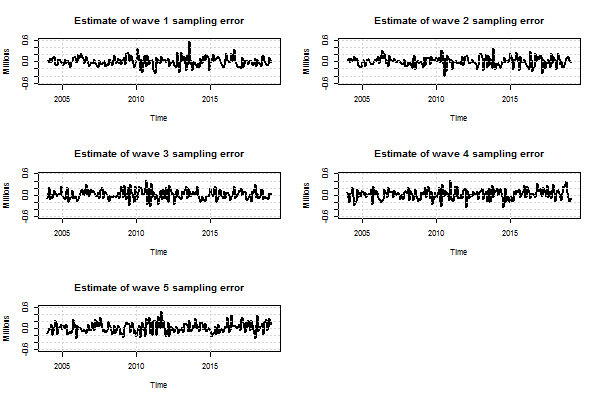
Source: Office for National Statistics - Labour Force Survey
Download this image Figure 5: Smoothed estimates of wave-specific sampling error for UK unemployment ages 16 years and over
.png (8.4 kB) .xlsx (25.4 kB)From the model, it is also possible to obtain estimated standard errors for each of the the estimated unobserved components. Figure 6 shows the standard errors for the estimated level of unemployment in the UK for ages 16 years and over, relative to the design-based standard error providing an indication of the gain in accuracy from using the model-based estimates.
Figure 6: Standard errors of smoothed and filtered estimates of the level of UK unemployment ages 16 years and over relative to single-month design-based standard errors
January 2004 to February 2019
Source: Office for National Statistics - Labour Force Survey
Download this chart Figure 6: Standard errors of smoothed and filtered estimates of the level of UK unemployment ages 16 years and over relative to single-month design-based standard errors
Image .csv .xlsThe monthly change in level from the design-based single-month estimates, as can be seen from the top panel of Figure 7 is volatile and rarely statistically significant, whereas the filtered and smoothed estimates provide clearer indications of change. The main benefit of these new experimental outputs is providing improved estimates of month-on-month change, which can allow earlier indication of turning points in the data.
Figure 7: Month-on-month change in the level of UK unemployment ages 16 years and over
Confidence intervals (99%, 95%, 90%, 75% and 50%), from design-based estimates (top), filtered estimates (middle) and smoothed estimates (bottom)
Source: Office for National Statistics - Labour Force Survey
Download this image Figure 7: Month-on-month change in the level of UK unemployment ages 16 years and over
.png (12.8 kB) .xlsx (76.7 kB)6. References
Brakel, J. van den, and S. Krieg. 2009. Structural Time Series Modelling of the Monthly Unemployment Rate in a Rotating Panel (PDF, 448KB).
Commandeur, J.J.F., and S.J. Koopman. 2007. An Introduction to State Space Time Series Analysis. Practical Econometrics Series. Oxford University Press, Oxford.
Durbin, J., and S.J. Koopman. 2001. Time Series Analysis by State Space Methods. Oxford Statistical Science Series. Clarendon Press.
Harvey, A.C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press.
Helske, Jouni. 2017. KFAS: Exponential Family State Space Models in R. Journal of Statistical Software Volume 78 (10), pages 1 to 39. doi: 10.18637/jss.v078.i10.
Office for National Statistics. 2016. Labour Force Survey User Guide: Volume 1 - LFS Background and Methodology 2016 (PDF, 1.76MB).
Office for National Statistics. 2019. Single Month Labour Force Survey Estimates: May 2019.
Pfeffermann, Danny, Moshe Feder, and David Signorelli. 1998. “Estimation of Autocorrelations of Survey Errors with Application to Trend Estimation in Small Areas.” Journal of Business and Economic Statistics Volume 16, pages 339 to 348.
R Core Team. 2016. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.
Skinner, C., and D. Holmes. 2000. Variance Estimation for Labour Force Survey Estimates of Level and Change: GSS Methodology Series 21.
Nôl i'r tabl cynnwys7. Appendix
Model specification
The observed monthly wave-specific estimates, yi,t ( i = 1,...5) comprise a population process (Yt) that is common to each estimate and a wave-specific error, ei,t such that:
State space framework
This section provides details of the structure of the multivariate state space model. State space models enable the estimation of unobserved components of multivariate time series. The models developed here aim to estimate an underlying stochastic population process and survey error processes, all of which are unobserved. The models used are linear Gaussian models.
The state space framework comprise an observation equation and transition equation. The observation equation shows how the unobserved components combine to form the observed values, and the transition equation shows how the unobserved components evolve over time following a first-order Markov process. Following the notation of Harvey (1990) and simplifying slightly to show only aspects that are relevant to the current study the observation and transition equation are respectively:
The observations, yt, are multivariate time series with N elements. The state vector of unobserved components is given by αt with dimension m × 1. The observation matrix that combines the unobserved components, Zt is of dimension N × m and the observation errors, ϵt, is a N × 1 vector. In the transition equation, Tt is the m × m transition matrix, which defines how that state vector changes over time, Rt is a m × q matrix determining which elements in the state vector are stochastic, and the transition error, ηt is a q × 1 vector.
Zt, Tt, Rt, Ht and Qt are system matrices that are non-stochastic. However, they may change over time, hence the time subscript, and can contain estimated values, for example, the hyper-parameters. For details on the estimation of unobserved components using the Kalman filter and methods for hyper-parameter estimation see, for example, Harvey (1990), Durbin and Koopman (2001) or Commandeur and Koopman (2007).
The models in this article are estimated using the KFAS package of Helske (2017) in the software R, R Core Team (2016). The optimiser used in R from the function optim provides various methods of optimisation based on Nelder-Mead, quasi-Newton and conjugate-gradient functions. In this article BFGS (a quasi-Newton method) is used.
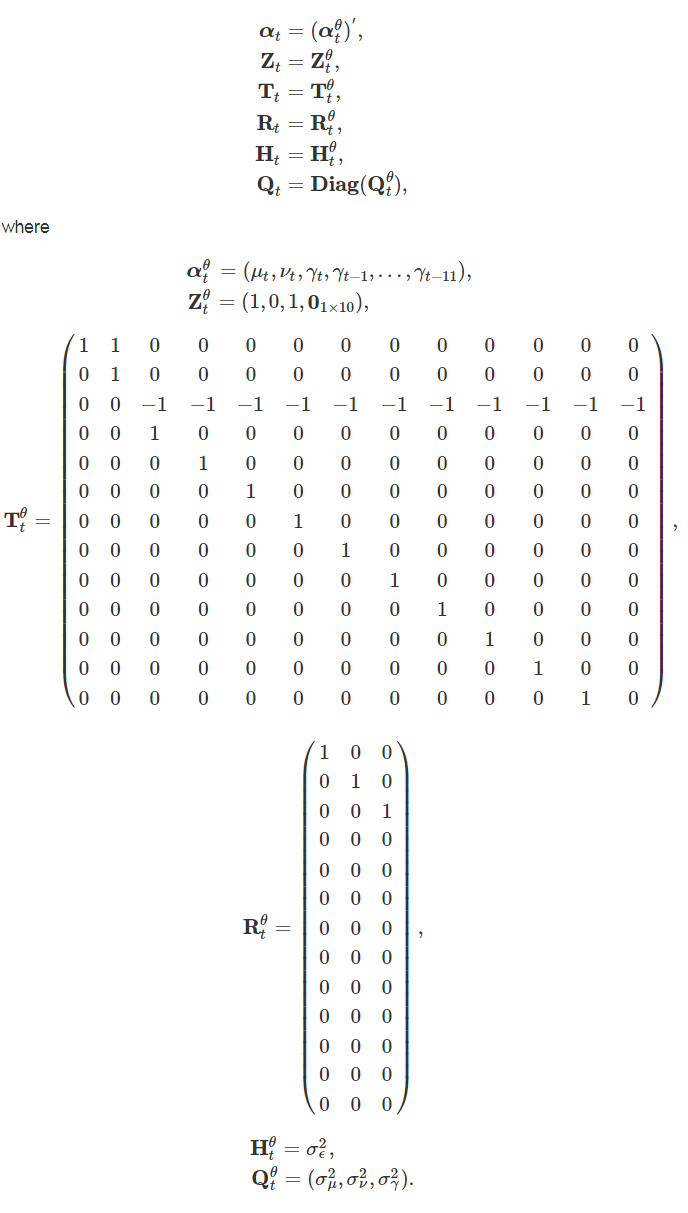
A univariate basic structural model given by yt = μt + γt + εt includes models for the trend and seasonal component, as described previously, with the irregular component (εt) as white noise. These equations can be expressed in state space form for monthly data with the state vector and system matrices given by:
θ denotes the population process as further components are included in the following models, and rn×m is a matrix of dimension n × m where each element is equal to r, In is an n × n identity matrix, Diag creates a diagonal matrix from the elements in parentheses, and BlockDiag creates a block diagonal matrix from the elements in parentheses, following a similar notation to Brakel and Krieg (2009).
If we assume that the observation error is actually the survey error then the observation error can be set to zero and the survey error becomes a component to estimate in the state vector. The design-based variance estimates, kt2, can be used to account for the changing variance over time as discussed by Brakel and Krieg (2009) . The state vector and system matrices for this model become (ignoring for now sample error autocorrelation):
Note that in this instance σϵ2 should equal one as discussed by Brakel and Krieg (2009).
When the observed design-based estimates are monthly wave-specific estimates and assuming the wave-specific survey error and bias terms are combined with the basic structural model in state space form.
If it is assumed that an autoregressive process of order 3( i − 1) for wave i, with parameters set to zero for any lags j ≠3( i − 1) for i = (2, ...,5) then the wave-specific survey errors can be modelled as:
In order to be able to model these relationships in the transition equation this requires many lags of survey errors, which results in a 31 × 31 transition matrix for the survey error part. This matrix is not written out due to its size, but the appropriate modifications to this and the other relevant system matrices are straightforward, given the previous equations.
Nôl i'r tabl cynnwys