1. Introduction
How can PAYE RTI help in measuring employment and earnings?
As Pay As You Earn (PAYE RTI) data cover the whole employee population (for those paid through PAYE), rather than a sample, they can be used to produce more precise and detailed statistics on pay and employment than the current survey-based statistics. Conversely, the statistics that can be produced from PAYE data are limited by the data that the PAYE system collects and rules under which it operates. While the Office for National Statistics (ONS) uses International Labour Organisation (ILO) definitions for its survey-based statistics, these cannot be adhered to so precisely using PAYE data, which are primarily collected for tax purposes.
Certain properties of the PAYE RTI data are unique among short-term indicators in the UK. For example, the ability to produce monthly statistics on the distribution of pay has not previously been possible. The additional details provided by these statistics on the status of the UK labour market has the potential to help inform decision-making across the country.
A comparison of ONS survey-based labour market statistics on pay and numbers of employees, and those produced using PAYE RTI statistics (including examination of the coverage and methodological differences) is included in this article.
These statistics may also have the potential in the future to replace some of those based on surveys, which could reduce the burden on businesses taking ONS surveys.
Why do we need new methods to produce monthly estimates using PAYE RTI?
PAYE RTI data include a record of payments employers make to their employees, and can be used to construct statistics on employee jobs and earnings. HM Revenue and Customs (HMRC) has published quarterly Experimental Statistics based on these data until recently. A quarterly basis was used to address the impact on the series of varying numbers of weekly paydays each month.
The new methods outlined in this article allow the alignment of the data to the period in which work was done to be improved for weekly, bi-weekly and four-weekly payments in particular. This brings the treatment of these payments more in line with the European System of Accounts, ESA 2010 (PDF, 6.40MB) recommendations, and effectively converts a payments dataset more formally towards a dataset of jobs and pay rates. As a result of new methods being applied to the data, monthly employee jobs and earnings statistics can now be produced.
The ESA 2010 requires that wages and salaries are recorded in the period during which work is done, rather than the time that earnings are paid to employees. The new methodologies estimate the period of work to which every payment corresponds. This results in a highly detailed micro-dataset which is better aligned to ESA 2010 principles, and from which time series can be generated through aggregation.
This is coupled with an estimation of pay rates, based on the payment amount and the frequency of payments, allowing for better comparison of pay for jobs paid at different intervals. Where work is paid weekly, for example, the pay rate for a job will no longer be affected by whether there were four rather than five paydays in the month.
This article will also explore the methodologies involved in imputing data for more recent time periods - where the data can be incomplete at the time of extraction - as well as adjustments made to make the data more suitable for producing statistics, such as improving estimates taking into account start dates, leaving dates, and varying pay frequencies.
Nôl i'r tabl cynnwys2. Calendarisation
What is calendarisation and why is it necessary?
Calendarisation is the process of converting PAYE payments into daily employment pay rates that can then be used to produce monthly employment counts and income, based on the estimated period of employment which each payment remunerates. For example, if payment was made on 5 February for employment in January, then the aim of the methodology would be to record an employment lasting throughout January, with a pay rate based on the payment received on 5 February. This aims to better align the data with the European System of Accounts (ESA) 2010 recommendation that wages and salaries should be measured in the period in which work is done.
The previous Experimental Statistics on jobs and earnings using Pay As You Earn Real Time Information (PAYE RTI) were produced on a tax quarter basis reflecting the fact that PAYE operates on a tax year basis (6 April to the following 5 April). In addition, data were allocated to a time period based on the date of payment, rather than the date of work done. While the two concepts are similar when allocating data to a quarter, their difference becomes more notable when creating monthly time series.
The calendarisation methodology outlined in this article transforms the RTI data for each payment from the date of payment to more broadly covering the period in which we estimate work to have been done. In doing this, the data as a whole become better aligned with recommendations in the ESA 2010, which in turn means the data are more comparable with those from the UK National Accounts. Importantly, when coupled with an estimation of pay rates – based on the payment amount and pay frequency – this methodology substantially reduces the volatility of time series produced using RTI data.
The calculation of pay rates, the amount paid per common unit of time, enables easy comparison of pay across jobs with different pay frequencies. This approach of measuring pay can be contrasted with measuring pay as the simple sum of payments amounts over a particular period. The latter can be problematic when aggregating data for jobs paid monthly and jobs paid weekly, as the number of weeks can vary in a month (as well as the number of particular weekdays which fall in a given month).
For example, an employee who is paid weekly on Fridays will have been paid four times in October 2019 and five times in November 2019. This employee would have been paid more in November when compared with October, while their pay rate – their weekly pay – may be the same. This effect broadly balances out in quarterly statistics, because generally quarters have 13 weekly paydays, but it is acute when calculating monthly pay time series.
Combining calendarisation with this method of calculating pay rates generates a near-continuous dataset of what jobs existed on any particular day, and the pay rate (converted to pay per day) for each job. This conversion from a dataset of payments to a dataset of jobs and pay rates enables the production of monthly statistics that better reflect labour market conditions, rather than the noise from variance in the number of paydays per calendar month. These methods are applied to the microdata, at the level of each payment. This enables simple aggregation to produce time series aggregates and the creation of an analytical micro-dataset consistent with these time series.
It is worth noting that this methodology aims to allocate pay to the period of employment which is being remunerated. While this is a similar concept to the “period of work done”, it may differ in certain cases. For example, someone who was a paid employee working weekdays would be recorded as employed continuously, including on weekends. Alternatively, someone on paid leave, a period during which no work was done, would also be classed as employed for that period. For simplicity, reference is made in this article to estimating the “period of work done”, but these caveats should be borne in mind.
The calendarisation methodology
Before converting the data from period of payment to the estimated period of work, the payment amount is transformed into a pay rate. A pay rate is essentially a daily rate of payment for a job, and is calculated by dividing the payment by the average length of the work period. For example, weekly pay is divided by seven, while monthly pay is divided by 30.4 (that is 365 divided by 12). The purpose of calculating this daily rate is to ensure that pay can be aggregated across employments with different pay frequencies – between those paid weekly and those paid monthly, for example.
To estimate the period of work for a payment using payment dates, it is initially assumed that payments are made entirely in arrears, that the payment date is the last day of the work period and the work period begins the day after the previous payment.
Limits are placed on the length of the resulting period of work, based on the employment’s pay frequency. If a work period appears too long or short, a default work period length is used based on the pay frequency.
For example, if an employment has a weekly pay frequency and two payments – one on 1 June and one on 15 June – then the latter payment would be deemed to correspond to a work period of 9 June to 15 June.
For the first payment of an employment, the reported start date will be considered when calculating the beginning of the work period. Provided that start date generates a work period that is not too long or short according to the job’s reported pay frequency, then it will be used as the first day of the work period, with the payment date as the final day.
The assumption that the payment date marks the end of a work period is relaxed in the case that an employment’s leaving date is recorded. More information on this is available in the section on Adjustments to the data.
The calculation of pay rates and work periods in effect creates a daily dataset of all those currently employed along with their respective rate of pay. This is then aggregated on a daily basis to calculate employment totals and pay statistics, and subsequently averaged over the calendar month to provide monthly aggregates. As a result, the monthly statistics produced can be interpreted as averages of underlying daily aggregates.
An important implication of this methodology is how it handles jobs which begin or end part way through a month. If in an employment begins halfway through a month, for example, it will be counted as half a job for the month as a whole. This will not affect the calculated pay rate for the employment. For example, if a job pays £100 a month and begins on 16 April, the pay rate for this employment will still be £100 a month when calculating average pay for April. The shorter work period will be reflected in the employment effectively being given a weight of a half when calculating average pay in April, to reflect that the job only existed for half the month. In addition, when calculating average employment for the month of April, these data would be counted as half a job.
Nôl i'r tabl cynnwys3. Adjustments to the data
Start dates
The start dates for employments collected through Pay As You Earn Real Time Information (PAYE RTI) can be used to improve our estimate of the first work period of an employment.
The data contain a relatively large number of start dates listed as the 1st or 6th of the month. These start dates can appear statistically implausible when considering the day of the week on which they imply employment began. Those reporting starting on the 1st or 6th can imply an unlikely high probability of beginning employment on a weekend, although they might also be specific to some areas of business. While this does not significantly impact on the operation of PAYE, the data could be improved for the purposes of statistical production. As a result, start dates which report being on the 1st or the 6th are not used to calculate improved work period estimates.
Pay frequencies
Employers have a range of options when supplying information about how often they pay employees. The possible pay frequencies for employees include weekly, fortnightly, four-weekly, monthly, quarterly, bi-annually and annually.
Occasionally, the gap between payments in the data appears to be different to the stated pay frequency. This may reflect circumstances such as unpaid leave, and there are other cases where the time between payments is consistent from one payment to the next, but does not match the reported pay frequency. While this will not affect the operation of PAYE as long as payments have otherwise been recorded correctly, amending the pay frequency recorded in the statistical data to reflect the actual pay frequency observed in the data can improve the functioning of the calendarisation methodology.
This is done as follows: if the time between payments does not align with the reported pay frequency three times in a row, but over that period consistently aligns to another pay frequency, then the pay frequency is amended accordingly.
Missed and double payments
“Employment”, for the purposes of these statistics, is defined as paid filled employee jobs. The processing outlined so far would result in a missed payment being translated into a missed period of work. In some instances the data can be used to infer that a missed period represents an unusual payment situation which does not correspond to a missed period of work.
One such instance is that in which a missed payment is followed by a payment that is near to double an employment’s usual amount, followed by a subsequent payment which returns to near the usual amount. This pattern appears to reflect a delayed payment rather than a period of missed work. The payment that is near to double the normal amount can then be deemed to cover two work periods, and processed as such.
The same processing is applied where the timing of the double payment is reversed, that is, where it precedes a missed payment. This may be the case when, for example, an employment which is usually paid in arrears is paid in advance for a single month. Again, such a case can be processed as if the payment corresponds to two work periods instead of one.
Payment in advance
When ensuring that payment data are aligned with the period in which work has been done, it is also important to know the extent to which work has been paid in arrears or in advance. This has been calculated for those who have left their jobs. The amount of advance pay can be approximated by finding the difference between the ratio of the length of their final period of work to their standard work period, and the ratio of final pay to standard pay.
Currently, this approximation of pay in advance is only applied to previous payments for those who have left their jobs. And to better ensure that any adjustment to work period is based on advanced payment rather than, for example, a bonus and normal fluctuation in pay, restrictions are placed such that payment amounts must be stable in the penultimate periods in order for this adjustment to be made. In future, it could be applied to non-leavers based upon factors such as their industry or payment date.
Nôl i'r tabl cynnwys4. Imputation
In order to produce timely statistics, the Real Time Information (RTI) data used in the estimation are extracted in the weeks following the end of the reference month. This will mean the dataset is incomplete, as for some individuals, payments relating to work done in that month are yet to be received. To produce reliable, unbiased statistics on a timely basis, imputation is required for recent periods in order to account for these reporting habits.
While survey data methods largely rely on sampling frames to impute and weight data, the RTI dataset has no such sampling frame. As such, the following methodologies have been developed, establishing a framework which uses and preserves the various unique features of the RTI dataset while meeting the needs of users of aggregate time series.
Two main features of the data need to be imputed – the existence of employments, and their level of pay. For the existence of employments, two different approaches are taken:
For those employments which have not recorded a leaving date, but not yet reported their next payment, a probability of existence is calculated for each respective subsequent payment.
To properly account for the population of “new” employments, a combined methodology is proposed. First, a survey-like approach is used, weighting reported data to estimate aggregates. This is then accompanied by a synthetic data-like approach for creating new employments which – when aggregated together with the reported data – will produce the estimated aggregates.
Once the existence of employments for each group is processed, their pay is then estimated. Where previous payment amounts for an employment are available, pay growth estimates are calculated and applied to the reported amounts for previous payments to calculate pay for these imputed observations. For the population of “new” jobs, a combination of survey-like and synthetic-like methods are used, in a similar fashion to that used to calculate employments.
Estimating employment using probabilistic imputation
For every job which has reported a payment over the last year, but has not reported a leaving date, payments are imputed at regular intervals carrying on from the last received payment, along with an estimation of the likelihood that the payment exists. When these imputed payments correspond to payment dates prior to the date on which the statistics are being produced, this equates to estimating the likelihood that the payment was made but has not yet been reported to HM Revenue and Customs (HMRC). When the imputed payment date is later than the date on which the statistics are being produced, this equates to estimating the likelihood that a payment will be made in the future.
Several factors can affect the likelihood that a job will be continued to be paid, but for the purposes of this methodology, two main variables are used: length of time since the previous payment date, and pay frequency. The former is important as, broadly speaking, the longer the amount of time since the last payment was received, the less likely it is that another payment will be received. In this context, it is also important to account for pay frequency. While there may be a high probability that a monthly paid job will receive another payment when the previous payment came in 25 days ago, there might be a lower probability if it has been 25 days, but the job is paid weekly.
To calculate these likelihoods, historical data are used to calculate the probability that, at t days after the payment date, given a leaving date has not been submitted, and conditional on the pay frequency of the job, a next payment would be received. This gives a series of probability weights which can be attached to the imputed payments.
In addition to this, using a similar methodology, an adjustment is made for the possibility that the job still exists and will be paid in the future but, for a number of reasons (such as unpaid leave), may have experienced a period of missed payments.
To summarise, for jobs which have previously submitted a payment to HMRC but have not submitted a leaving date, their last payment is “carried forward” – in effect copied and pasted (possibly several times depending how often the job is paid, but with the payment date changed with increments corresponding with the job’s pay frequency). For each of these new, imputed payments, a probability weight is created which represents (based on historical data) an estimate of the probability that the job has continued and payment or payments made.
Estimating employment and payment amounts for new jobs
New jobs by definition do not have a history of payments. The lack of information on past payments which could be “carried forward” to use in the imputation methodology described above means that a different approach is required to impute first payments for new jobs.
Instead, submissions relating to new jobs – received before the extract was drawn or would have been drawn for the system run – are treated as a (biased) sample. Throughout this section, these submissions are referred to as “pre-extract submissions”, which should not be confused with a judgement as to whether the submission was submitted to HMRC before the date it is due.
While standard statistical methodology would use a sampling frame to derive weights for data to ensure representativeness of the population, no such frame is available for RTI. Instead, historic pre-extract submission rates are used to derive grossing weights, and so produce summary statistics. These summary statistics are then used, alongside a synthetic data-like approach, to produce a microdata set that reproduces these summary statistics, alongside other dimensions of the data.
To begin, past data are analysed to calculate, relative to their payment date, what portion of information on payments had been received each day (that is, what portion is received five days before the date of the data extract, four days before the date of the data extract, and so on). This is done by pay frequency, and by the day of the month on which the payment is made. So, for example, a calculation is made for the average portion of monthly payments received 10 days before payment date, where said payment date is the 15th of the month.
This produces a set of submission rates by pay frequency, day of the month on which payment is made, and date of receipt relative to the payment date. These submission rates can then be inverted to produce grossing weightings, and merged on to the incomplete new jobs data for the periods which need imputation. By using these grossing weights, estimates can be made of total new job payments and average payments amounts for the periods being imputed.
To account for potential bias in average payments amounts of pre-extract submissions, historical data are again analysed to estimate average bias based on the receipt date of payments relative to their payment date – controlling for pay frequency and the day of the month on which the payment falls. These are then used to calculate bias adjustments for pay in the periods under imputation, which are applied to the data for the purposes of calculating average payment amounts.
For some payment dates needing imputation, the submission rate may be too small to use a grossing based methodology. For example, to calculate pay rates for work done in the latest month, it is necessary to calculate payments for annually paid people which will be made in just under a year’s time. If the analysis of historic submission rates show that responses for a particular pay frequency would be below 5% for a particular period, then a macro-based nowcast and forecast is incorporated to calculate new-job payments and average payment amounts for the period. For the time being, this nowcast simply carries forward the growth rate from the previous period.
Once summary statistics are estimated for each pay frequency in each pay period, a “synthetic-data”-like approach is used to create microdata which will be used alongside real receipts to reproduce these summary statistics, and replicate other characteristics of the data. The purpose of this is to account for dimensions of our data – such as the distribution of pay – which are not accounted for by the grossing methodology, and which might differ between those who file their RTI submissions on a more timely basis and those who do not.
Synthetic data, as defined by the US Census Bureau, are “created by statistically modelling original data and then using those models to generate new data values that reproduce the original data’s statistical properties”. The data we wish to produce are imputed observations for those data submissions not yet received.
A good proxy for these, in terms of replicating the attributes of this group, are those who would not yet have submitted data at the same time last year. So, for example, if data are being produced on 15 January 2020 for new job payments in January 2020, then – when imputing for people who will submit data after 15 January 2020 – a good proxy for the properties of these data are those employees for whom data for January 2019 was submitted after 15 January 2019.
In this fashion, duplicate observations are created based on new job payments which would not have been received at this point in previous years, but with their payment dates altered to match the pay periods being imputed.
The summary statistics (of total payments and average payment amount) can then be used to constrain these synthetic-like data so that – when combined with the actual filings received – the summary statistics are reproduced. The resulting microdata should now better represent the statistical properties of the final data – and will be less biased toward, for example, only reflecting the pay distribution of those whose data are submitted pre-extract. It also means that actually submitted data will not be edited. So if, for example, pre-extract submissions were known to be upwardly biased, then this will be accounted for by the imputed post-extract submissions having a correspondingly offsetting downward bias. This is essential to the production of coherent distributional statistics – such as medians and percentiles – alongside averages and totals.
The effect and reasoning for this process can be visualised using Figure 1, which shows an illustrative example of the distribution of pay for new jobs. It aims to show what the data might look like when the extraction date is substantially earlier than the reference period.
Figure 1: Example decomposition of the distribution of pay for new jobs, by whether the submission was submitted before or after the extract was drawn
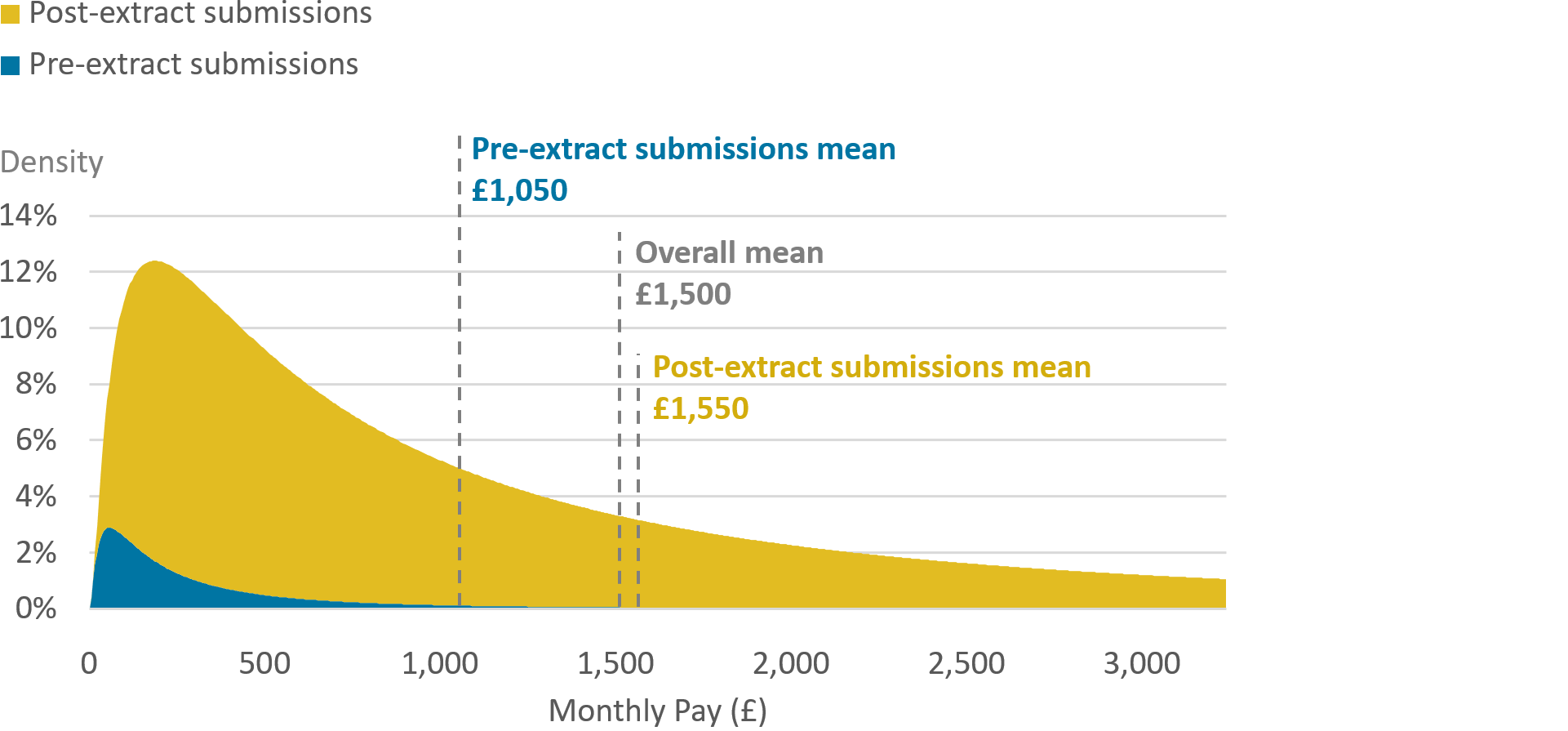
Source: Office for National Statistics
Notes:
- This chart has been constructed for illustrative purposes only and is not based on actual RTI data
Download this image Figure 1: Example decomposition of the distribution of pay for new jobs, by whether the submission was submitted before or after the extract was drawn
.png (71.6 kB)First, the chart could be considered as showing how the real, full data might look once all tax returns have been received. Pre-extract submissions make up a portion of the chart, as do post-extract submissions . The dimensions of the data for these two groups can differ. For example, the mean pay of each group can differ – in this example, pre-extract submissions have a mean pay of £1,050, and post-extract submissions have a mean pay of £1,550. Once each is weighted by the respective size of each group, the overall mean is obtained – in this example, £1,500.In addition to means differing, the shapes of the distribution for each group can differ as well. In this example, the distribution of pre-extract submissions is more skewed than are post-extract submissions.
This difference of the shape of the distribution between pre- and post-extract submissions is an example of a feature of the data which would be difficult to impute using grossing weights alone. Unless the data are stratified according to pay level when calculating grossing weights, the eventual shape of pay distribution may not be well imputed.
Stratification is the process of splitting the data up by characteristics, and is used in many weighting methodologies to account for uneven representation along those characteristics in a dataset. For example, if a survey is known to be biased towards sampling more younger people than older people, the data may be stratified by age when weighting in order to give a higher weight to older people, and as a result, be representative of the population under examination. In the example of Figure 1, pre-extract submissions are more skewed than the post-extract submissions, and (without stratification by pay band) so any distribution of grossed-up pre-extract submissions would also be overly-skewed. This point extends to other features of the data for which there may be bias in the pre-extract submissions, on which the grossing is not stratified – for example geographies or industries.
Adding strata to the grossing process for all the features of the data for which statistics might want to be calculated would result in low data quality, or would be impossible. This approach would require a sufficient amount of pre-extract submissions within each strata. In the case of survey data, non-bias can often be assumed for many features of the data – after controlling for some broad non-random characteristics through stratification – because of a designed randomness in the sampling procedure.
As the pre-extract submissions are not a survey, the randomness of this “sample” cannot be assumed. Given the several features of the statistics we wish to publish now or in the future, there is a resultantly high number of strata which would be required, and a sufficient sample size would be needed for all of them. This cannot be assured for all periods needing imputation, particularly for payments in the future.
Figure 1 can also be used to illustrate the way our methodology seeks to avoid this issue, by adding synthetic-like data to our pre-extract submissions. Pre-extract submissions, can be used to calculate the average for that group. By looking historically at the relationship between average pay of pre-extract submissions, and the eventual total average pay, a bias adjustment can be calculated. Using this bias adjustment, the overall mean can be estimates for the period. By knowing the typical proportion of the data which are pre-extract , we can estimate how much of the data we have not yet received, that is, post-extract submissions. Using this, alongside our average pay for pre-extract submissions and the overall mean, we can estimate what average pay would be for the post-extract submissions.
The creation of synthetic-like data then happens by taking the post-extract submissions from the same time last year, adjusting their pay so that they hit the estimate for this period’s post-extract submissions, and adding them to our dataset for this period. Combined, these two adjustments ensure that our imputed and non-imputed data together hit our grossed and bias adjusted estimates of new job counts and new job average payments. This process is performed separately for each payment frequency.
By combining pre-extract submissions and synthetic-like estimates of post-extract submissions, the features of the post-extract submissions are carried forward from previous years – features like pay distribution, geographies, industries and so on. the data are still adjusted based on the pre-extract submissions so that, to some extent, the economic factors which have affected the pre-extract submissions are also reflected in the synthetic-like data.
In the case where a nowcast is used, where the submission rate for pre-extract submissions is too low, then this process is broadly unchanged. However, instead of using bias-adjusted pre-extract submissions to estimate the overall mean pay, that is, mean pay for both submissions made before and after the system’s run this is done by nowcast.
Estimating payment amounts for continuing jobs
In a similar methodology outlined for new jobs, when imputing payment amounts for continuing jobs, historical response rates are used to gross up pre-extract submissions with a bias adjustment applied.
For continuing jobs, an important piece of information is already available for every job – the last payment amount submitted. The task of imputation for continuing jobs resultantly becomes imputing what the change in payment amount should be.
Pre-extract submissions are used to estimate a bias-adjusted average payment growth for a particular payment date. Using the same methodology outlined in the Estimating employment and payment amounts for new jobs section, this is then used to estimate the average payment growth rate for payments which have not yet been received, that is those that require imputation. Once this average has been calculated, it is then applied to the previous payment for each job being imputed, and the result is the imputed payment amount for this job on the particular payment date. This process happens separately for all pay frequencies.
By combining the probabilistic weight calculated for each job without a leaving date – outlined in the Estimating employment using probabilistic imputation section – and the payment amounts calculated in this section, microdata is constructed for continuing jobs which can be aggregated to calculate both pay and employment.
Nôl i'r tabl cynnwys5. Areas for development
These are experimental statistics and will continue to sit in a developmental phase. This does not mean that the quality of the statistics is low, but rather that the statistics are still novel and may be improved further. We are publishing these statistics now to enable users to benefit from work done so far, and also to offer users an opportunity to comment on their development.
Future improvements to these statistics will be informed by user feedback. Below are examples of development under consideration, but are not intended to present an exclusive or exhaustive list.
Refining calendarisation and imputation methodologies
By analysing the outputs of the calendarisation and imputation methodologies outlined in this article, we hope to refine them further over the coming months through incremental development. Within this article, several of these possible developments have been mentioned – such as using regression-based nowcasting in the imputation methodology. These changes would leave the framework of the calendarisation and imputation methodology outlined in this article unchanged, but could improve aspects of it.
Improving work period definition
In the section on adjustments to the data, we discussed the adjustment to payments which considered the extent to which they were made in advance or in arrears. Because of the need for a leaving date, this adjustment can only be calculated for those jobs which have ended.
While the individualised version of this methodology is only possible for jobs which have ended, by analysing patterns in these jobs a generalised adjustment could be calculated, dependent on characteristics related to the extent to which a job tends to be paid in advance.
Start dates
There is another adjustment that affects start dates, given the improbability of the number of start dates listed as being on the 1st or 6th of the month. Currently, all employments with a start date listed as the 1st or 6th of the month are imputed, but a future development may be able to utilise other data to better determine whether a start date of the 1st or 6th is in fact an exact representation of the precise start date. For example, if an employer lists all start dates as the 1st, this may be less likely to be accurate, although it might be specific to their area of business. In contrast, if an employer has a wide array of reported start dates, one of which being the 1st or 6th of the month, it may be more likely that this particular job did actually start on that date, and the start date would not need to be imputed.
Investigating strata definitions for imputation process
The imputation methodologies outlined took account of important features of the data, such as pay frequency and the day of the month on which the payment was made, when calculating grossing weights. However, when calculating summary statistics to use in imputation, these statistics are calculated for the entire population. Imputation may be made, on average, more accurate for each payment being imputed by instead splitting the population by various characteristics which may affect payment amounts – such as geography and industry – when calculating grossing weights and summary statistics.
Developing a “core” pay measure
While Pay As You Earn Real Time Information (PAYE RTI) data do not separate bonuses from other payments including regular pay, it may be possible to process the data for each job to strip out unusual movements. Such movements could be because of bonuses, but could also be because of paid overtime, arrears, or other one-off factors. Resultantly, the series which is created would not constitute “regular pay” in the same sense as statistics such as average weekly earnings, but might provide some of the same utility – that of a less volatile, “core” pay measure.
Using the more longitudinal element of the data
In recent years, more attention has been bought to the utility of summarising and analysing the pay growth (or pay loss) individuals receive – such as in, for example, the latest Annual Survey of Hours and Earnings. By looking, for example, at median growth in pay instead of growth in median pay, the effects of compositional effects for the changing structure of the workforce are reduced. This can mean that median growth in pay is a more useful measure of “pay inflation”, and so provides a helpful indication of the macro-economic climate.
PAYE RTI data would enable the production of statistics like this on a timely basis. In the future, we aim to explore the most beneficial way to utilise this longitudinal aspect of the data to meet user needs – and would welcome feedback on this.
Nôl i'r tabl cynnwys6. Comparisons with other labour market statistics
How to interpret differences between these Experimental Real Time Information Statistics and other sources of labour market statistics
It is important to point out that the statistics in this methodological article are experimental, and users of labour market statistics are recommended to use the Office for National Statistics (ONS) Labour market release as the definitive source of UK National Statistics on the labour market.
Two additional items that users of labour market statistics may find useful are A guide to labour market statistics and A guide to sources of data on earnings and income.
There are certain limitations in using administrative data to produce statistics which can make comparisons with other sources of statistics difficult. These can be caused by a difference in content, for example, where the data from the administrative system do not measure the same statistical concept that is measured by a survey. Or alternatively, they can be because of coverage differences, where the administrative data cover a different population than the one covered by the survey.
When comparing the statistics in the accompanying PAYE RTI publication to the established labour market statistics, the Average weekly earnings (AWE) series and the Annual Survey of Hours and Earnings (ASHE) for employee income, and the Labour Force Survey (LFS) for employee numbers, these limitations mean that the different series are not directly comparable.
More information on the issues caused by content and coverage of administrative data is available from the UK’s Office for Statistics Regulation.
Comparisons of employee numbers between PAYE RTI and the Labour Force Survey
The number of people receiving pay from PAYE employment reported by these Experimental Statistics is higher than the Labour Force Survey employment series for all months. This is likely to be because of differences in coverage and content between the two series. As the Labour Force Survey (LFS) estimates are based on survey data, they are subject to sampling variability. The coverage and content differences which will generally result in the RTI estimates being higher than the LFS, while sampling variability in the LFS results may affect the comparison in both directions.
Differences in Coverage
The RTI data include all individuals who have an employment in a PAYE scheme and who received remuneration for activity in the reference period. This will cover a wider population than the LFS which does not include individuals under 16 years, foreign resident individuals and people temporarily staying in the UK. Additionally, the sampling frame for the LFS is UK residential addresses and communal establishments, with the exception of NHS accommodation, are not sampled. The difference between the household population used to gross the LFS and the resident population was estimated to be 470,000 based on comparisons between the March 2011 LFS and the 2011 Census.
The LFS will also have better coverage of the undeclared economy as the RTI data only include information on employments that are known to HMRC. Finally, RTI classifies any person with an employee job as being an employed person, whereas LFS only classifies a person as being an employee if their main job is an employee job.
Differences in content
The LFS data are collected via an interviewer, providing the opportunity to clarify what information is required to answer the questions. Employment status is then assigned based on the responses to these questions. The RTI data are collected through the employers’ legal obligation to provide PAYE information to HMRC. Extensive guidance is available for employers explaining what information they are required to submit and, in addition to other checks, the main figures will be scrutinised by employees checking that they are receiving the correct pay.
The LFS uses the International Labour Organisation (ILO) definition of employment, while the PAYE RTI statistics are based on individuals receiving pay. The PAYE-based figures are an average of the estimated number of employees in paid employment on of each respective day of the month, while the LFS series is based on respondents who carried out at least one hour’s paid work within a reference week. The LFS estimates are then calculated as averages of those employed in the reference weeks across the three-month period.
Additionally, the LFS employee figures used in this publication only include those whose main employment source of income is from an employee job, and exclude those whose main activity is self-employment, with work for an employer as a secondary activity. This may be a small factor in the LFS series being lower than RTI, because of the additional inclusion in the RTI figures of individuals whose main employment income source is self-employment but who have a secondary employment source.
Non-response and sampling variability
The Office for National Statistics (ONS) invests significant effort and resources into obtaining high response rates in the survey data. However, non-response may introduce biases that need to be adjusted for, and this is done using methods such as imputation or through reweighting the received responses. These adjustments can be compared with the (relatively small) grossing adjustments made to the RTI data in the tail of the series.
The effects of non-response and the fact that the LFS is based on a sample means that as with all sample surveys, estimates from the LFS have a sampling error attached to them. A statistic (for example, an estimate of a mean or a total from a random sample) will be subject to sampling variation; its value will vary from one sample to the next if repeated random samples are drawn.
| Labour Force Survey (LFS) | Real Time Information (RTI) | |
|---|---|---|
| Timeliness | Published monthly. A six- to seven-week gap between the end of the reference period and the publication date. | Published monthly. A six- to seven-week gap between the end of the reference period and the publication date. |
| Employment measure | Anyone carrying out at least one hour’s paid work in the reference week. | Anyone who has a paid employee job during the reference period. |
| Reference period | One week. | A monthly average of daily estimates. |
| Inclusions | UK resident population in · private households · NHS accommodation · young people living away from parental home in a student hall of residence or similar institution during term time | All individuals receiving pay through a PAYE scheme. This will include: · people living in communal establishments · some foreign residents · people aged under 16 years |
| Exclusions | · employees not paid during the reference period, for example,for certain types of seasonal work (summer or Christmas jobs) · people aged under 16 years · communal establishments such as residential care homes, prisons or defence establishments · foreign residents | · employed individuals in the undeclared economy whose income is not reported to HMRC via PAYE · self-employed · members of PAYE schemes where no employee earns above the Lower Earning Limit for National Insurance or has another job |
| Full-time/part-time breakdown | LFS collects data for all employees, full-time and part-time employees separately. | RTI does not differentiate between full-time and part-time workers. |
| Statistical adjustments | Non-response – imputation on rolling forward previous data from the respondent and reweighting of responses. | Calendarisation, imputation, and other adjustments outlined in this article. |
| Sampling variability | For employees aged over 16 years, plus177,000 for July to September 2019. | Not applicable. |
Download this table Table 1: The main differences between the Labour Force Survey and Real Time Information
.xls .csvComparisons between RTI and LFS statistics
The LFS employee series excludes employees whose main income source is self-employment, causing the LFS series to be lower than RTI.
Figure 2, shows a comparison of a three-month moving average of the headline RTI employees series and the headline LFS employee series (which already uses a three-month moving average).
Figure 2: The number of employees is consistently higher in Real Time Information (RTI) than in the Labour Force Survey (LFS)
Number of employees for Real Time Information and the Labour Force Survey, UK, seasonally adjusted, three months to September 2014 to three months to October 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Labour Force Survey
Download this chart Figure 2: The number of employees is consistently higher in Real Time Information (RTI) than in the Labour Force Survey (LFS)
Image .csv .xlsFigure 3 shows the growth rates of employment in RTI and LFS compared with the same month of the previous year. Over the past five years as a whole, the two series show a broadly similar rate of employment growth. However, the two have shown different short- and medium-term movements.
Figure 3: Employee growth can vary between the Labour Force Survey (LFS) and Real Time Information (RTI)
Annual employee growth rates for Real Time Information and the Labour Force Survey, UK, seasonally adjusted, three months to September 2015 to three months to October 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Labour Force Survey
Download this chart Figure 3: Employee growth can vary between the Labour Force Survey (LFS) and Real Time Information (RTI)
Image .csv .xlsComparisons between RTI and AWE measures
The ONS has two main sources of earnings statistics, the Annual Survey of Hours and Earnings (ASHE) and the Average weekly earnings (AWE) series, which is produced from the Monthly Wages and Salaries Survey (MWSS).
AWE is the ONS’ lead indicator of short-term changes in earnings. It is designed to capture monthly changes in the average weekly earnings of employees in Great Britain. AWE is based on the Monthly Wages and Salaries Survey, which covers employees working in businesses with 20 or more employees in all industrial sectors in Great Britain (an adjustment is made for smaller businesses using ASHE data). As this is done monthly, there is much less detail than the yearly ASHE.
Because of the different methodologies of AWE and RTI, the headline statistics for mean pay are not directly comparable. In a distribution such as earnings where the higher end is skewed because of a small percentage of very higher earners, the mean will be higher than the median. Like RTI, AWE also includes the earnings of those whose earnings were reduced for any reason which will have the effect of reducing the mean figure. In addition, both RTI and AWE will include anyone who has been added to a payroll for just a month, for example to receive a bonus or similar.
Comparisons between RTI and AWE
Both mean and median earnings are published in the RTI statistics, but only mean pay is available for AWE. The RTI estimates include the earnings of those employees whose earnings were reduced for any reason. Additionally, the RTI statistics cover Northern Ireland, HM Armed Forces and government-supported trainees paid via PAYE, pay-rolled redundancy payments and signing on fees, all of which are excluded from AWE.
Another important difference is that RTI estimates are calculated on a person basis while AWE estimates are calculated on a job basis. As people can have more than one job – in which case the pay from their multiple jobs would be summed together in RTI – this difference will cause the RTI estimates to be higher than the AWE estimates.
Sampling variability
As with the LFS, AWE will be subject to sampling variability, which will also lead to differences between the RTI and AWE estimates.
| Average weekly earnings (AWE) | Real Time Information (RTI) | |
|---|---|---|
| Timeliness | Published monthly. A six- to seven-week gap between the end of the reference period and the publication date. | Published monthly. A six- to seven-week gap between the end of the reference period and the publication date. |
| Employment definition | Anyone with a live employment on a PAYE scheme in the reference period. | Anyone who has a paid employee job during the reference period. |
| Reference period | One month, and some information is collected based on pay frequency. | A monthly average of daily estimates. |
| Average measure | Mean. | Mean and Median pay from PAYE, number of individuals receiving pay from PAYE. |
| Bonuses | AWE captures bonus payments in every month of the year, with bonuses peaking between December and April. Bonuses are identified separately to regular pay in AWE. | All bonus payments paid via PAYE are included although they can be difficult to differentiate from normal payments in the data. |
| Inclusions | · regular pay · bonuses · overtime · shift premium · allowances (weekly or monthly allowances are included in regular pay, annual allowances are included in bonus pay) · employees on trainee or junior rates of pay · employees whose earnings were affected by absence | RTI covers all income from PAYE so will include the following if paid via PAYE: · regular pay · bonuses · overtime · shift premium · allowances · arrears · employees on trainee of junior rates of pay · employees whose earnings were affected by absence · payrolled redundancy payments · payrolled signing-on fees · payrolled expenses |
| Exclusions | · Northern Ireland · self-employed · HM Armed Forces · government-supported trainees · employer National Insurance contributions · employer contributions to pension schemes · benefits in kind · expenses · redundancy payments · signing-on fees · stock options not paid through payroll | · self-employed · stock options not paid through payroll · employer National Insurance contributions · employer contributions to pension schemes · benefits in kind (except payrolled benefits in kind) · earnings for members of schemes where no employee earns above the Lower Earning Limit for National Insurance or has another job |
| Full-time/part-time breakdown | AWE does not differentiate between full-time and part-time workers. | While RTI does collect some banded information on hours worked, it doesn’t specifically differentiate between full-time and part-time workers. |
| Statistical adjustments | Non-response reweighting of responses. Businesses with fewer than 20 employees are not sampled; they are estimated using a factor derived from ASHE. | Calendarisation, imputation, and other adjustments outlined in this article. |
Download this table Table 2 : The main differences between Average Weekly Earnings and Real Time Information
.xls .csvComparisons between RTI and AWE headline statistics
As the RTI statistics are presented as mean monthly pay, this been divided by 4.3482, as this is the average number of weeks in a month. Figure 4 shows that mean weekly pay is slightly higher in the RTI series than in AWE.
Figure 4: Mean weekly earnings are consistently higher in Real Time Information (RTI) than in average weekly earnings (AWE)
Average weekly earnings for Real Time Information and Average Weekly Earnings, UK, seasonally adjusted, three months to September 2014 to three months to October 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Monthly Wages and Salary Survey
Notes:
- RTI data covers the UK, AWE data is Great Britain only.
Download this chart Figure 4: Mean weekly earnings are consistently higher in Real Time Information (RTI) than in average weekly earnings (AWE)
Image .csv .xlsFigure 5 shows the growth in mean weekly pay for each month compared with the same month a year earlier. The series suggest relatively similar growth rates over the past five years, but can show a difference in short-term movements.
Figure 5: Mean weekly earnings growth can vary between Real Time Information (RTI) and average weekly earnings (AWE)
Percentage growth on same three months in previous year, UK (Real Time Information) and Great Britain (Average Weekly Earnings), seasonally adjusted, three months to September 2015 to three months to October 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Monthly Wages and Salary Survey
Notes:
- RTI data covers the UK, AWE data is Great Britain only.
Download this chart Figure 5: Mean weekly earnings growth can vary between Real Time Information (RTI) and average weekly earnings (AWE)
Image .csv .xlsComparisons with ASHE
Alongside AWE, the Annual Survey of Hours and Earnings (ASHE) is another important ONS source of earnings statistics. ASHE is produced on an annual basis, using a reference day in April. It can be used to analyse earnings by industry, occupation, region, geography down to parliamentary constituency level, sex, and full- or part-time status.
Headline ASHE statistics focus on gross weekly earnings for full-time employee jobs on adult rates of pay whose pay in the reference period was unaffected by absence. This differs from RTI in that RTI does not differentiate based on full-time or part-time job status, and will include those whose work was affected by absence. The most comparable statistic to RTI is ASHE data on median gross weekly earnings of all employees surveyed, including those who work part-time.
Differences in content
ASHE is based on a 1% sample of employees, sampled from HMRC PAYE data in January of the same calendar year. The January sample is updated with HMRC data supplied to the ONS in April to take account of new entrants to the Labour market, and those who have changed jobs since January. While the sample is employees, ASHE is completed by the employer.
| Annual Survey of Hours and Earnings (ASHE) | Real Time Information (RTI) | |
|---|---|---|
| Timeliness | Published annually. There is a six-month lag between the reference period and when the data are published. | Published monthly. A six- to seven-week gap between the end of the reference period and the publication date. |
| Employment definition | Those who are employed for the reference date in April, based on a 1% sample of jobs from the HMRC PAYE register from the January of the same year. | Anyone who has a paid employee job during the reference period. |
| Reference period | The ASHE reference date is in April each year. Weekly (and hourly) statistics relate to the employee’s pay period in which the ASHE reference date falls. | A monthly average of daily estimates. |
| Average measure | Mean and median. | Mean and median. |
| Bonuses | ASHE collects information on bonuses; there are some concerns about their inclusion, as the information may not be available to respondents at the time they are required to submit information. | All bonus payments paid via PAYE are included although they can be difficult to differentiate from normal payments in the data. |
| Inclusions | · bonuses and incentive pay (relating to the pay period only) · overtime · shift premium pay · other pay (such as car or on-call allowances) | RTI covers all income from PAYE so will include the following if paid via PAYE: · bonuses · overtime · shift premium · allowances · arrears · employees on trainee or junior rates of pay · employees whose earnings were affected by absence · payrolled redundancy payments · payrolled signing-on fees · payrolled expenses |
| Exclusions | · self-employed · HM Armed Forces · government-supported trainees paid via PAYE · company directors who do not receive a salary · employees working offshore (for example, oil rig workers) · those not on adult rates of pay · employees whose earnings in the pay period were affected by absence (for example because of sickness) | · self-employed · stock options not paid through payroll · employer NI contributions · employer contributions to pension schemes · benefits in kind (except payrolled benefits in kind) · earnings for members of schemes where no employee earns above the Lower Earning Limit for National Insurance or has another job |
| Full-time/part-time breakdown | Differentiates between full-time and part-time employee jobs. | While RTI does collect some banded information on hours worked, it does not specifically differentiate between full-time and part-time workers. |
| Statistical adjustments | ASHE results are weighted to account for non-response and the number of jobs given by the Labour Force Survey (LFS). The data are imputed for non-response. | Calendarisation, imputation, and other adjustments outlined in this article. |
Download this table Table 3: The main differences between the Annual Survey of Hours and Earnings and Real Time Information
.xls .csvComparisons between RTI and ASHE headline statistics
ASHE’s headline statistic of pay is median gross weekly pay of full-time employee jobs, for employees on adult rates of pay and whose pay was unaffected by absence in the reference period. ASHE also publishes statistics on all workers, rather than just those who work full-time. This is more comparable with RTI. As ASHE uses a reference period within April each year, the most comparable RTI figure is the (non-seasonally adjusted) median weekly pay for April of each year.
Figure 6 shows median weekly pay from RTI and ASHE. ASHE is consistently higher. One reason for this may be the exclusion of workers with absences, and those not on adult pay rates in the ASHE data. Additionally, the RTI figures may be higher because they measure pay per person, while the ASHE data measures pay per job. As a person can have several jobs – in which case the pay from each job is summed for a person in the RTI data – pay per person will be higher than pay per job.
Figure 6: Median weekly earnings are consistently higher in the Annual Survey of Hours and Earnings (ASHE) than in Real Time Information (RTI)
Median Weekly Pay for RTI and ASHE, UK, non-seasonally adjusted, April 2015 to April 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Annual Survey of Hours and Earnings
Download this chart Figure 6: Median weekly earnings are consistently higher in the Annual Survey of Hours and Earnings (ASHE) than in Real Time Information (RTI)
Image .csv .xlsFigure 7 shows growth of median weekly pay from both sources. Although there are few data points to compare, the two broadly show the same trends over the period.
Figure 7: Growth in median weekly earnings are broadly similar in the Annual Survey of Hours and Earnings (ASHE) and Real Time Information (RTI)
Median Weekly Pay growth rates for RTI and ASHE, UK, non-seasonally adjusted, April 2016 to April 2019
Source: HMRC – Pay As You Earn Real Time Information and Office for National Statistics – Annual Survey of Hours and Earnings
Download this chart Figure 7: Growth in median weekly earnings are broadly similar in the Annual Survey of Hours and Earnings (ASHE) and Real Time Information (RTI)
Image .csv .xlsManylion cyswllt ar gyfer y Erthygl
labour.market@ons.gov.uk rtistatistics.enquiries@hmrc.gov.uk
Ffôn: +44 (0)1633 455400 +44 (0)3000 593779
