Cynnwys
- Main points
- Overview
- Defining our target classes: updating the classification structure to introduce new data sources
- Obtaining a large labelled dataset
- How consistent are humans at labelling?
- Machine learning classification models
- Measuring the performance of our machine learning classification models
- Classifier performance: what is good enough?
- Future classification research
- Annex A: Comparing ML methods
- Related links
1. Main points
In this article we cover research undertaken to use machine learning algorithms to automatically classify clothing data, scraped from retailer websites, to produce consumer price indices.
To maximise use of our alternative data sources, we introduce “consumption segments” as an additional level in the index hierarchy, allowing us to maximise classification performance while ensuring item homogeneity is high enough to produce reliable and unbiased indices.
We have created a dataset of over 50,000 manually classified clothing products, to train and test the performance of machine learning algorithms in the classification of web-scraped clothing data; investigations into the consistency and error in human classification reveal that our labellers consistently classify products in 88.8% of cases – many inconsistencies were because of ambiguities in clothing classes, rather than explicit error.
We use a gradient-boosted tree machine learning algorithm (XGBoost) to present results from our currently best-performing classifier, showing a macro-averaged precision of 0.79, but this score is weighed down by some low-performing consumption segments.
We compare results of price indices for four clothing items constructed using machine-predicted classifications from five different algorithms, finding high-performing classifiers show little divergence in the resulting indices.
2. Overview
New data sources and methods are being introduced into the production of consumer price statistics from 2023. The new data sources, namely web-scraped and scanner data, have the potential to improve the quality of UK consumer price statistics through increased coverage and more timely data. Both these new data sources cover a much wider range of products, and at larger frequencies and quantities, than is possible with any form of manual price collection.
Data collected using traditional methods are manually classified to our existing consumer price statistics hierarchy so that there is a high degree of certainty in the classification of products. However, it is not feasible to manually classify the volume of data that we are obtaining from these new data sources.
Research into new, automated, methods of classification is therefore a high priority. Several different methods are available ranging from simple “keyword” classifiers, which link to an item category based on a single keyword in a product name, to more complex methods using supervised machine learning algorithms that identify unseen patterns in the data.
The applicability of these methods depends on the data source, for example, scanner data (which tends to have less attribute information available), may be better suited to simpler techniques that do not require a lot of additional descriptors to help identify what category a product might belong to.
Different categories of item may also require different techniques, for example technological goods are quite easy to distinguish (that is, it is either a smartphone or it is not), whereas clothing has a mixture of different items within its broad description (for example, it could be a dress or a pair of trousers).
The use of automated methods for the purposes of classification for consumer price statistics is becoming increasingly studied by national statistical institutions. Countries such as the Netherlands, Norway (Word, 250KB) and Belgium (PDF, 339KB), to name a few, have been active in publishing research in this area. The UK is also taking part in a UN Task Force on Scanner Data, for which classification of alternative data sources is a major topic of interest.
This article covers some of the research that we have completed to date to use supervised machine learning algorithms to efficiently and accurately classify web-scraped clothing data. Since November 2018, we have been receiving web-scraped data for several items including clothing. In any one month the web-scraped data for clothing alone contain in excess of 900,000 unique clothing products. This compares to approximately 20,000 clothing products collected each month using traditional, manual methods.
We are planning to use the experience gained from this research to apply to our other targeted priority categories, as well as continue to research other methods such as the keyword classifier.
Nôl i'r tabl cynnwys3. Defining our target classes: updating the classification structure to introduce new data sources
The UK classification structure, currently known as the European Classification of Individual Consumption according to Purpose (ECOICOP), is relatively broad1 . Therefore, beneath this level we have our own sample of representative “item”-level definitions that are unique to the UK. For example, the lowest level of ECOICOP may be “women’s garments” but within this we may collect the garments “women’s formal shirt”, “women’s casual shirt”, “women’s full-length leggings” and a range of other women’s garments deemed representative of consumer spending.
There are no strict internationally defined restrictions as to what these item-level definitions should be, but the CPI Manual: Theory and Practice (PDF, 5MB) suggests that an elementary aggregate should consist of expenditures on a small and relatively homogeneous set of products, defined within each consumption category. For example, a women’s formal shirt would need to be in a different item category to women’s leggings as they are used for different purposes, but a blue women’s shirt and a red women’s shirt may be grouped as the same item, given they are typically used for the same purpose. We describe items as being more “homogeneous” when products are similar in nature and used for similar purposes.
Data collected using traditional methods use samples from tightly defined item definitions to represent the wider market. For example, blouses which open fully at the front are chosen as being representative of all women’s blouses. Replicating these tight definitions with alternative data sources would be both extremely challenging from a classification perspective, and undesirable as it would not make full use of the data available. Therefore, for web-scraped and scanner data we introduce broader “consumption segments”, in this case a “women’s blouse”, without specifying whether it needs to open fully at the front.
Consumption segments can be designed at different levels of homogeneity. For example, dresses can be classified to a broader “dresses” segment or to several narrower segments such as “casual dresses”, “occasion dresses” and “work dresses”. However, there is a balance to be made; although the narrower segments are more homogeneous, they may also be more difficult to classify towards since the rules needed to split these types of dresses are likely to be more complex than simply identifying a dress.
Human classifiers that generate the labelled training data may also struggle to distinguish between casual and work dresses from just a text description, and if the machine receives poor training data it will likely make poor classifications. Our goal is to ensure classification performance is high enough to produce reliable and unbiased indices while also maximising homogeneity of the consumption segment.
As alternative data sources are being used to complement traditional collection methods, and traditional methods will remain sample-driven, we will continue to collect prices for a representative item, or items, within each consumption segment for our traditional collection. In the scanner and web-scraped data, however, we intend to move towards collecting all products within a consumption segment to maximise use of the dataset and improve our market coverage.
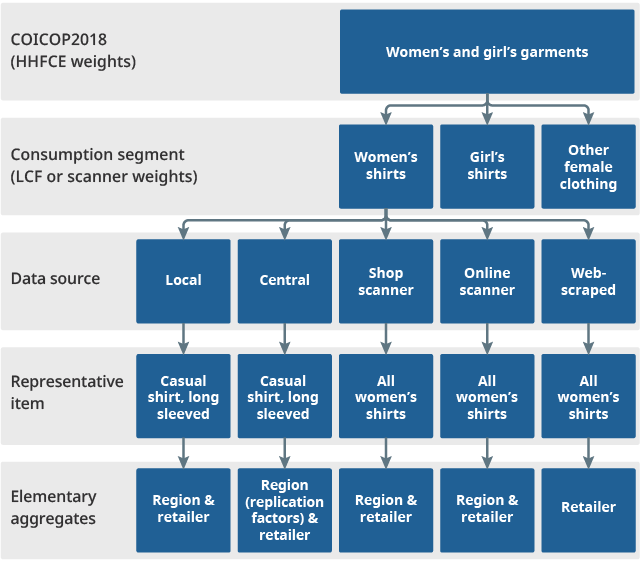
Data from different regions, store types and data sources will be aggregated to form a price index at the consumption segment level, which is then combined with indices from other consumption segments to form the higher-level aggregate consumer price indices. The proposed future aggregation structure for the consumer price inflation baskets is shown in Figure 1. This is the aggregation structure below the lowest level of the COICOP 2018 hierarchy, where there is less guidance as to how elementary aggregates should be formed. This shows how we plan to use the scanner and web-scraped data in future, to supplement the existing traditional (local and central) collections.
Figure 1: Proposed future aggregation structure for CPIH and CPI below the lowest level of the COICOP hierarchy
Source: Office for National Statistics
Download this image Figure 1: Proposed future aggregation structure for CPIH and CPI below the lowest level of the COICOP hierarchy
.png (40.7 kB)For the remainder of this article we focus on the COICOP 2018 subclasses “Garments for men or boys”, “Garments for women or girls” and “Garments for infants (0 to under 2 years)”. Within these subclasses, we have currently defined 85 broad clothing consumption segments to classify to. The number of consumption segments we use is likely to expand during this research phase as our samples of labelled data increase, allowing us to classify to a more granular hierarchy.
Notes for: Defining our target classes: updating the classification structure to introduce new data sources
- A newer version of COICOP, COICOP 2018, has recently been released, and we are working towards this new classification structure in our alternative data sources work.
4. Obtaining a large labelled dataset
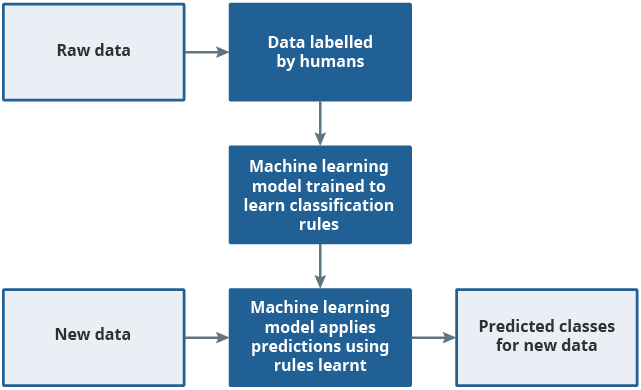
Supervised machine learning (ML) models require a dataset containing several features (predictor variables) and a set of data that has already been classified to the desired category (labelled data) and are trained to learn rules that associates the two. These rules are then applied to new, previously unseen data to make predictions on the correct classification. This process is shown in Figure 2.
Figure 2: Supervised machine learning uses labelled data to learn rules which are then applied to new unseen datasets
Source: Office for National Statistics
Download this image Figure 2: Supervised machine learning uses labelled data to learn rules which are then applied to new unseen datasets
.png (18.5 kB)To build a supervised ML model, we first manually classify a sample of products to the clothing consumption segments, creating a human-labelled dataset. This dataset is split into a training dataset, from which the model can learn its rules, and a test dataset, from which we can test the performance of the predictions made by the model.
If we were to label a random sample of products, then we would expect the labelled dataset to have many women’s shirts and very few boys’ gilets. The model trained would likely have much greater success at identifying women’s shirts compared to boys’ gilets. To improve the balance between the two (and other types of clothing), we use stratified sampling with weights proportional to the number of consumption segments in that age and gender group (boys’, girls’, infants’, men’s, women’s). For example, as 22 of our 85 segments are women’s, we require 26% of the web-scraped clothing sample data to be women’s. This attempts to account for there being a wider variety of women’s clothing types sold, relative to boys’ clothing types. We then stratify with equal weight the retailers and retailer hierarchy from each age and gender segment to cover all product types and all retailers. In Section 9 we discuss active learning for a more efficient sampling procedure as part of our future work.
For this analysis we have used a human-labelled dataset containing 1% of six months of web-scraped clothing data, equating to over 54,000 unique products. This was achieved by upwards of 30 people within the Office for National Statistics (ONS) Prices Division labelling clothing data using a bespoke labelling application that we developed in house. Labellers label the data at multiple levels of granularity, allowing us to compare classification performance at different levels of homogeneity. The six currently sampled months are spread across the year to ensure seasonal variations in clothing are accounted for. We have tried to ensure that our human-labelled data are as consistent as possible using the bespoke labelling application, training for human labellers, and a detailed frequently asked questions (FAQ) document.
Nôl i'r tabl cynnwys5. How consistent are humans at labelling?
Despite our best efforts to ensure consistency amongst human labellers, there is an element of subjectivity in clothing classification. For example, a “hooded jacket” can be considered both a “hoodie” and a “jacket”. If high levels of inconsistency are occurring, then the machine will not be able to reliably predict how to classify products. To quantify any inconsistencies between our human labellers, 12 labellers manually classified the same 313 clothing products to consumption segments, without consultation.
Since the placement of products can be somewhat subjective, we treat the chosen majority as being the correct consumption segment. For example, if 11 people have labelled a product as a “dress” and only one person has labelled it as a “skirt”, then we would assume dress to be the correct consumption segment.
Figure 3 shows that, on average, labellers were consistent with the majority consumption segment in 88.8% of cases. Most labellers were closely distributed, showing between 88% and 92% consistency with the majority consumption segment. Consistency with the majority consumption segment was always greater than 81%.
Figure 3: Around 89% of labels are consistent across human labellers

Source: Office for National Statistics
Download this image Figure 3: Around 89% of labels are consistent across human labellers
.png (9.3 kB)Figure 4 shows for each product, the number of labellers who have chosen the majority class. For more than half of the products, all twelve labellers agreed on how to classify the product, and all but one labeller agreed in a further (approximately) 20% of cases.
Figure 4: There was a broad consensus on how to classify most products
Source: Office for National Statistics
Download this chart Figure 4: There was a broad consensus on how to classify most products
Image .csv .xlsThe products that split opinion the most strongly were unsurprisingly often products which were on the boundary of two possible classes. This suggests that some of the inconsistency is driven by subjectivity in how to place cases that could belong to more than one class rather than labellers making explicit errors. Example products include:
- “fleece zip through jacket” (fleece=5 / jacket=5 / waterproof=2)
- “sporty hooded jacket” (hoodie=2 / sports jacket=5 / jacket=5)
- “[sports brand] zip top” (sports top=4 / sports jacket=4 / other=3 / t-shirt=1)
Further inconsistencies were seen in products that were ambiguous with regards to their pack contents. For example, a product was described as a “two-piece jogger set”. How labellers classified this product was dependent on what the labeller perceived “two-piece” to mean: a two-pack of jogging bottoms; or a full tracksuit, including a top and a pair of jogging bottoms.
As well as these ambiguities, some explicit labelling errors were also observed. For example, one product was described as “floral print shorts (30 waist)” with no further supplementary information. Some labellers did not pick out that a “30 waist” is typically a men’s size in British clothing standards and labelled the product as unisex.
We can use this information to refine our guidance to our human labellers. But while consistency of labelling can be improved through further training and detailed guidance, there remains a limit as to how consistent our labels can be, given the subjective nature of some clothing items as we have seen.
This “ceiling effect” in consistency therefore also provides something of a benchmark for our automated classification models. We are unlikely to accurately classify every product through either manual or automated classification, but we can strive for our automated classification to classify products to the same level of consistency as our human labellers have demonstrated.
Nôl i'r tabl cynnwys6. Machine learning classification models
Each consumption segment is made of an age and gender group and a clothing type. This includes, for example, “infants’ sleepsuits”, “men’s socks” and “girls’ dresses”. Since age and gender are important in unpicking the consumption segment to which a product belongs, we use text mining to obtain features (predictor variables) that may indicate gender or age. For example, if a clothing product comes with the size “mg” (medium girls’), this would indicate that the product is for non-infant girls. We also use various standard word embeddings for our features, including FastText, TF-IDF and bag-of-words. A more thorough view of these word embedding features can be found in the Ottawa Conference paper (PDF, 1.61MB).
We are using these features along with our human-labelled data to train and test the performance of machine learning (ML) models. There are many ML algorithms that have been developed to perform classification tasks. Not all algorithms are suitable for all datasets or tasks, and different algorithms have different levels of complexity and transparency. A comparison of results for several algorithms can be found in Annex A. For this article we primarily demonstrate results based on gradient-boosted trees (specifically XGBoost), as these are currently our highest-performing algorithm.
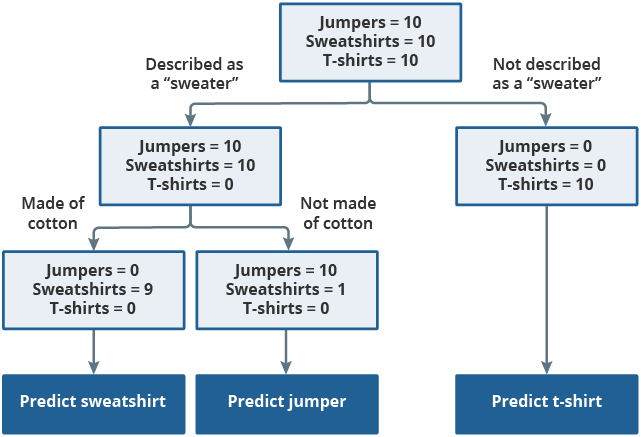
XGBoost uses decision trees as a foundation. A decision tree can conceptually be thought of as a flowchart, as displayed in Figure 5. When training the tree, every product starts in a single node (represented by the top rectangle). Products are continually split into two new nodes using automatically generated binary (yes/no) decisions, the “rules”. The goal is to keep splitting the tree until the final nodes mostly represent a single consumption segment. These rules are then applied to new, previously unseen, data to make predictions as to the correct product classification.
Figure 5: Decision trees use binary decisions to split the data
Source: Office for National Statistics
Download this image Figure 5: Decision trees use binary decisions to split the data
.png (27.2 kB)Decision trees are among the most basic classification algorithms and are relatively poor performers for complex classification tasks. However, they can be trained very quickly so are often used in ensemble models, such as gradient-boosted trees. An ensemble model involves training numerous classifiers and then using them in conjunction to provide a final decision on classification.
Gradient-boosted trees (such as the XGBoost algorithm used in our analyses) involve training many decision trees sequentially, with each tree trained to improve on the errors made by previous trees. Predictions of the final ensemble model is therefore the weighted sum of the predictions made by all previous tree models.
Nôl i'r tabl cynnwys7. Measuring the performance of our machine learning classification models
As we have seen, even with well-trained machine learning (ML) classification models it is unlikely that the predictions will be accurate 100% of the time given the ambiguities in clothing data and imperfect human-labelled datasets. To be able to include these classifiers in our official UK consumer price statistics we must have appropriate metrics in place to measure and monitor classifier performance over time. We also need to provide a performance threshold that a classifier will need to exceed in order to be used and understand the impact of classification inaccuracies on our consumer price statistics.
There are numerous metrics to quantify classifier performance on a dataset, each with different properties. In earlier work, we published an article for the Technical Advisory Panel on Consumer Prices (PDF, 1.2MB), discussing the appropriateness of various classification metrics. For this article, we focus on two lower-level metrics:
Precision: measures the purity of a consumption segment. A segment with 90% precision would mean 10% of the elements classified to the segment are from other segments (false positives).
Recall: measures the extent to which all cases from the consumption segment are captured by the classifier. A class with 90% recall would mean 10% of elements that should be part of the segment have been incorrectly classified elsewhere (false negatives).
There is a trade-off between precision and recall. To capture the trade-off between precision and recall, we report a third metric:
- F1: the harmonic mean of precision and recall. In this article, precision and recall are equally weighted. In future we may choose to weight precision as more important than recall, or vice versa, producing a more general F-score.
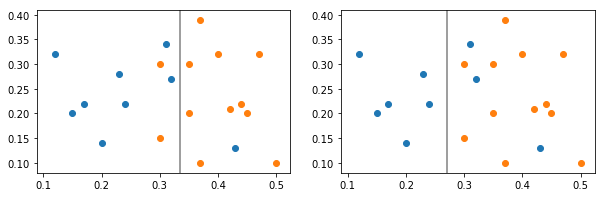
Figure 6 shows the trade-off between precision and recall. Two consumption segments are split by two different classifiers. Classifier 1 (left) splits the data to give greater recall for the blue class (it captures most of the blue cases, but is impure in that it also captures a couple of orange cases), whereas Classifier 2 (right) provides greater precision (it captures only blue cases, but a few blue cases are also lost to the orange class).
Figure 6: Classifier 1 gives the blue class better recall whereas Classifier 2 gives the blue class better precision
Source: Office for National Statistics
Download this image Figure 6: Classifier 1 gives the blue class better recall whereas Classifier 2 gives the blue class better precision
.png (6.8 kB) .xlsx (17.2 kB)By taking an average value (with equal weighting) for the precision, recall and F1 across all consumption segments, we can report classifier performance at an aggregated level. This method of aggregation is known as macro-averaging; other methods of averaging are also available and discussed in our Technical Advisory Panel on Consumer Prices article, but are not covered in this article.
In Table 1 we report on a small number of our 85 current consumption segments, alongside the macro-averaged figure across all 85 consumption segments. We see that there are some very high-performing consumption segments, but the macro-averaged F1 score is weighed down by some lower-performing consumption segments. Note that, for the results presented in this article, we have trained our models on three months of labelled data and tested our models on the remaining three.
| Precision | Recall | F1 | |
|---|---|---|---|
| Women's dresses | 0.95 | 0.89 | 0.92 |
| Women's jeans | 0.96 | 0.84 | 0.90 |
| Women's skirt/shorts | 0.88 | 0.80 | 0.84 |
| Women's sports bottoms | 0.71 | 0.57 | 0.63 |
| Women's suit jacket | 0.53 | 0.58 | 0.55 |
| Macro-averaged | 0.791 | 0.757 | 0.772 |
Download this table Table 1: XGBoost classifier performance of a small number of consumption segments
.xls .csvThe table gives an intuitive sense as to where some of the classification challenges lie. For example, the classification of jeans is high performing, likely because the classifier can often determine jeans simply through the word “jeans”. By contrast, sports bottoms use similar terminology to non-sports bottoms (such as “bottoms”, “shorts” and “leggings”), which may lead to confusion in the classifier, and worse performance.
Another challenge is the relative size of different consumption segments. There are many more dresses in our training dataset than suit jackets and the predictive performance likely reflects this. Figure 7 shows the relationship between the training set size and precision scores on the test dataset.
Figure 7: Classes with more training data generally classify better
Source: Office for National Statistics
Download this chart Figure 7: Classes with more training data generally classify better
Image .csv .xlsAs can be expected, segments with more training data generally perform better and we are expecting performance to continue to improve for several of our segments as we label more data. However, some segments perform relatively well on low volumes of training data and some segments perform relatively badly on high volumes of training data. For example:
- Infants’ outfit sets (represented by the orange dot on the right hand side of Figure 7) have high volumes of data and relatively poor precision; this likely reflects the variety within the class and the high overlap with other classes, for example, an outfit set that contains a t-shirt and jogging bottoms may cause the classifier to incorrectly identify the product as a t-shirt or jogging bottoms.
- Girls’ swimwear (represented by the orange dot on the left hand side of Figure 7) has low volumes of data and relatively high precision; this likely reflects that simple words such as “swimwear” are enough to identify such a broad category of swimwear because there is such a low overlap between swimwear and other classes.
The latter exception demonstrates the trade-off between the requirement for homogeneous consumption segments and classifier performance. Breaking down the swimwear class into swimsuits and two-piece swim sets will increase homogeneity but results in consumption segments with smaller amounts of training data, and it may require the classifier to learn more complex rules to distinguish between different swimwear types.
A confusion matrix can be used to compare the machine’s predictions against human labels. We can use confusion matrices to understand the consumption segments that the classifier is struggling to distinguish between. A small portion of our confusion matrix is available in Table 2, but the full version is available as a download. As might be expected, the ML classifier sometimes confuses Women’s suit jackets with Women’s outerwear jackets.
| Classifier prediction | |||||
|---|---|---|---|---|---|
| Girls' coat/jacket | Women's coat/jacket | Women's suit jacket | Other categories | ||
| Class given by labeller | Girls' coat/jacket | 197 | 1 | 0 | 37 |
| Women's coat/jacket | 5 | 167 | 14 | 44 | |
| Women's suit jacket | 0 | 9 | 29 | 12 | |
| Other categories | 29 | 31 | 12 | 21098 | |
Download this table Table 2. Confusion matrix for a small number of classes
.xls .csvIn an example from our wider confusion matrix, the classifier also often makes mistakes between male underwear and swimwear, likely since “trunks” can appear in both. Note that the classifier is generally quite good at distinguishing between age groups; there is little evidence of misclassification between girls’ coats and jackets and women’s coats and jackets. This may be because of the feature that targets age.
When exploring the consistency of human labelling, we saw that labellers are approximately 89% consistent in their labelling, setting a benchmark for what a classifier may be able to achieve. In this section we have seen that, currently, our best performing classifier achieves a macro-averaged precision score of around 79%.
There are several ways that we hope to improve our classification performance in some of the worst performing consumption segments. For example, we can increase our sample sizes and review our consumption segments so that they can be more easily defined. Our next steps for improving classifier performance can be found in Section 9.
Nôl i'r tabl cynnwys8. Classifier performance: what is good enough?
It is not realistic to expect that a machine learning (ML) model would be correct in every single instance. The question then is: when is a machine learning classifier perceived to be good enough for use in the production of consumer price statistics? The goal should be to produce a classification model, such that the indices formed on its predictions are close to the indices that would be produced if all classifications were correct. That is, classification performance is good enough to produce unbiased indices.
At present we do not have a long series of consecutive months of labelled data to compare indices based on our model predications against. Instead, we consider the closeness of the indices for four different Women’s clothing consumption segments (dresses and jeans are chosen as high-performing segments, sports bottoms and suit jackets are chosen as low-performing segments). These indices are produced based on classification predictions made by five different ML algorithms. These are XGBoost, Random Forest, Support Vector Machine, Logistic Regression and Decision Tree, descriptions of these methods are provided in Annex A. We compare indices using the rolling year GEKS-Jevons index method as this is currently our top shortlisted index number method for when expenditure data, or approximate expenditure weights, are unavailable.
As seen in Table 1, dresses and jeans classify relatively well using XGBoost, whereas sports bottoms and suit jackets classify relatively poorly. In Figure 8, we show the F1 score for these items using a range of automated classification algorithms.
Figure 8: High F1 scores are shown for dresses and jeans; low scores for sports bottoms and suit jackets
Source: Office for National Statistics
Download this chart Figure 8: High F1 scores are shown for dresses and jeans; low scores for sports bottoms and suit jackets
Image .csv .xlsNote that decision trees struggle with complex multiclassification tasks and performs much worse than the other four algorithms for each of these consumption segments. The four other classifiers perform relatively similarly, with higher scores for dresses and jeans and lower scores for sports bottoms and suit jackets.
The price indices presented in this section are experimental and should not be taken as official estimates of market behaviour for clothing. All graphs exhibit a downwards trend which is not necessarily true. Instead of focusing on specific numbers, we consider the closeness of the indices presented. These indices should not be taken as truth because of the product churn problem described in Research indices using web scraped price data: clothing data.
Figures 9a and 9b show price indices for our two high-performing classes: dresses (9a) and jeans (9b). Unsurprisingly, indices using products classified by decision trees behave differently to indices produced using products that have been classified by higher performing classifiers. This is likely because of the previously mentioned low classification performance of decision trees resulting from their overly simplistic design. Reassuringly, the four other classifiers result in relatively close indices for dresses and jeans, suggesting that they are likely classifying the same products.
Figure 9a: When classification performance is high (as for dresses), indices are tight and co-move closely, whereas decision trees are poor-performing classifiers and diverge
Source: Office for National Statistics
Download this chart Figure 9a: When classification performance is high (as for dresses), indices are tight and co-move closely, whereas decision trees are poor-performing classifiers and diverge
Image .csv .xls
Figure 9b: The classifier performs well at detecting jeans and the resulting indices are close
Source: Office for National Statistics
Download this chart Figure 9b: The classifier performs well at detecting jeans and the resulting indices are close
Image .csv .xlsFigures 10a and 10b show indices for two lower-performing classes: sports bottoms (10a) and suit jackets (10b). The differences between the indices are now more pronounced. This is particularly the case for suit jackets where misclassification combined with small sample counts leads to volatility in the indices. Despite being one of our lowest-performing classes, the indices for sports bottoms co-move reasonably well showing that the indices can be quite resilient to classification error.
Figure 10a: When classification performance is lower, the difference between the indices are more pronounced
Download this chart Figure 10a: When classification performance is lower, the difference between the indices are more pronounced
Image .csv .xls
Figure 10b: Poor classification performance paired with low sample counts can result in divergent indices, as is the case for women’s suit jackets
Download this chart Figure 10b: Poor classification performance paired with low sample counts can result in divergent indices, as is the case for women’s suit jackets
Image .csv .xlsFigures 9 and 10 show that higher classification performance generally reduces the variability in index values, showing the need to classify products well. However, there is a possibility that the four high-performing classifiers in Figure 8 are making the same errors, and these errors are causing a bias in the index. For example, it may be that all four classifiers make similar errors and fail to capture denim dresses (perhaps misclassifying them as jeans). If there is a rise or fall in the manufacturing costs of denim, the four indices presented would not be affected but the “true index” would.
To study this, we are working on labelling a consecutive time series of monthly data to compare our classification indices to a “ground truth index”. Note that this “ground truth” series would still be subject to errors and inconsistencies in human labelling as discussed previously.
Nôl i'r tabl cynnwys9. Future classification research
The primary focus of our work for improving our classification of web-scraped clothing data remains in the acquisition of human-labelled data. As shown in Figure 7, some consumption segments are being trained on low amounts of data and our desire to break these segments up further increases the demand for increased training data. Our current method of sampling data for human labelling is likely to be inefficient; we continue to sample more women’s jeans even though performance is already very high in this consumption segment. Therefore, we are researching the use of active learning. Active learning involves labelling products that the classifier can only predict with low confidence. By labelling the data that the classifier struggles the most with, we can accelerate the learning process with more efficient labelling. We are also exploring a data expansion method known as positive-unlabelled learning.
Machine learning is highly empirical. There are many hyperparameters (configurable options) in a machine learning pipeline that can be modified. While there exist rules of thumb guiding what good options for these parameters are, we will continue to explore optimal parameters to provide the highest possible performance for our clothing classification. We are also considering investigating the use of other classification algorithms such as neural networks.
We also continue to work on the features (predictor variables) used in the model to further enhance performance. For example, the classifier is worse at predicting sportswear-related classes (such as sports jackets, sports tops and sports bottoms). We may be able to create a feature determining whether there exists any sports-related terminology (such as sportswear, football, cricket and exercise) in the product name or description that the classifier may be able to use to improve performance.
We are planning to use the experience gained from this research to apply to our other targeted priority categories, as well as continue to research other methods such as the keyword classifier. Furthermore, to date, we have only focused on automating classification for web-scraped data, but we are also starting to explore automated classification of scanner data for grocery items, based on the early data feeds that we have received from retailers.
Nôl i'r tabl cynnwys10. Annex A: Comparing ML methods
In the main article, we focused on the results from XGBoost, a variant of gradient-boosted decision trees. This method obtained the highest macro-averaged precision score, although other methods performed closely. We chose to prioritise precision to ensure the products that we classified to each consumption segment were as “pure” as we could make them. We may choose to prioritise other metrics in future. In Section 8, we plotted indices using XGBoost, Decision Trees and three other methods.
Random Forests: another ensemble classifier involving decision trees. Different Decision Trees are trained on random samples of both training data and features. The class with the highest average confidence is taken as the classification. In contrast to XGBoost each of the trained trees are independent from each other. This has the advantage that they can be trained simultaneously potentially speeding up training times, but one tree cannot learn from another’s mistakes. In gradient-boosted tree models, the training data is reweighted after each tree is trained to attempt to help the subsequent trees perform better based on past mistakes. As gradient-boosted trees are dependent on each other this can make training slower but can give improved performance.
Support Vector Machines: aim to fit a hyperplane that separates the classes. The best fit hyperplane separates the classes with maximum margin between the hyperplane and the nearest data points of the different classes. These closest points are referred to as the support vectors. For an explanation of support vector machines, see Hastie and Tibshirani (2013), Chapter 9 (PDF, 11.4MB).
Logistic regression: separates the data into classes using a linear combination of input features. These predictions are converted to probabilities. The model then iterates to find the linear combination of features that produces a probability distribution most like the training data.
In Table 3, we now compare the macro-averaged results for each classifier. It is worth noting that we have not fully tuned each model, so these results should not be understood as the best possible results that the method may give using our training data.
| Classifier | F1-score | Precision | Recall |
|---|---|---|---|
| XGBoost | 0.772 | 0.791 | 0.757 |
| Support Vector Machine | 0.799 | 0.783 | 0.826 |
| Logistic Regression | 0.759 | 0.722 | 0.818 |
| Random Forests | 0.726 | 0.679 | 0.802 |
| Decision Tree | 0.42 | 0.389 | 0.487 |
Download this table Table 3: At the time of writing this report, our best classification results were obtained with XGBoost and Support Vector Machines
.xls .csvIt is worth noting that, aside from classification performance, there are other factors that go into how suitable a classification method is. For example, although Support Vector Machines are competitive in classification performance in this table, they are also (often) comparatively time-consuming to train and make predictions with which may make them less practical for use in production. There are other factors to consider such as interpretability, whether the method can provide a confidence score alongside its prediction and the resource needed to maintain the system. Our final assessment of the most appropriate method will also have to consider these factors.
Nôl i'r tabl cynnwys