Admin-based population estimates and statistical uncertainty: July 2020

We are committed to maximising our use of administrative data and reducing reliance on the decennial census. In 2019, a third version of admin-based population estimates for England and Wales (ABPE V3.0) was published as research statistics. This report provides insights on ABPE quality by considering measures of statistical uncertainty.

We define statistical uncertainty as the quantification of doubt about an estimate. Research into statistical uncertainty is conducted by Office for National Statistics (ONS) Methodology in collaboration with the University of Southampton Statistical Sciences Research Institute.

The ABPE V3.0 has produced population estimates for 2011 and 2016, building on knowledge gained from previous versions of the methodology, ABPE Version 1 (V1.0) and ABPE Version 2 (V2.0). The explicit design objective for ABPE V3.0 was to avoid population overcount, by introducing an "activity" based metric. The analysis presented in this paper shows that this has not been fully achieved.

The data suggest that in 240 local authorities there is at least one year of age for either males or females where the ABPE overcounts the population. There is overestimation at more ages in Inner London; for example, Newham, Tower Hamlets and Lambeth have overcount in ABPEs for 64, 48 and 39 single years of age, respectively.

For 65% of all ages, ABPE uncertainty intervals entirely contain the mid-year estimate uncertainty intervals, implying that they are both capturing the same "truth", by very different methods. This occurs more often for males (68%) than for females (62%).

ABPE overcount is concentrated among under-ones, children aged 5 to 18 years and pensioners. These ages need further investigation. 

There are characteristic patterns of undercount in the ABPE, particularly at student ages. In four local authorities, the ABPEs are at least 15% lower than our uncertainty measures suggest they should be.

The relationship between local authority mid-year estimates (MYEs) and ABPEs has shifted substantially between 2011 and 2016. ABPEs appear to align more closely with the MYEs in 2016 than they did in 2011, with 14% of ABPEs falling within the MYE uncertainty bounds in 2011 and 45% in 2016. Further research should investigate the relationship between the ABPEs and the true population count over time. 

The coverage assessment process for ABPEs will be challenging, particularly when time lags in the administrative data mean that people will be counted in the wrong place. We recommend that further design of the ABPEs, and the inclusion rules for each demographic group, should be closely informed by the proposed coverage assessment strategy for that group.

We would like to acknowledge Professor Peter Smith from the University of Southampton Statistical Sciences Research Institute who has helped us to develop the measures of statistical uncertainty described in this paper. We are also indebted to him for his comments and suggestions in the research and writing of this report.

The admin-based population estimates (ABPEs) are research outputs and not official statistics. They are published as outputs from research into a methodology different to that currently used in the production of population and migration statistics. As we develop our methods, we are also developing the ways we understand and measure uncertainty about them. These outputs should not be used for policy- or decision-making.

The admin-based population estimates (ABPEs) are produced through linkage of administrative data and the application of a set of rules in the attempt to replicate the usually resident population. The sources used in the ABPE Version 2 (V2.0) were the NHS Patient Register (PR), the Department for Work and Pensions (DWP) Customer Information System (CIS), data from the Higher Education Statistics Agency (HESA) and data from the School Census (SC). Records found on two of these four data sources were included in the population. This led to estimates that were higher than the official estimates, especially for males of working age.

The main design objective of the ABPE Version 3 (V3.0) was to remove records that were erroneously included in the previous method. An ABPE with under-coverage for all age and sex groups would be closer to unadjusted census counts and, when combined with a Population Coverage Survey (PCS), should allow dual-system type estimators to be applied with improved results. The new method thus uses a different approach – utilizing additional data sources and introducing stricter criteria for inclusion in the population.

The data sources used in the new method are:

• Pay As You Earn (PAYE) and Tax Credits data

• National Benefits Database (NBD) and Housing Benefit (SHBE) data

• Child Benefit data

• NHS PR and Personal Demographic Service (PDS) data

• HESA data

• English and Welsh SC data

• Births registrations data

The new criteria used for inclusion in the population are:

• a sign of activity within the 12 months prior to the reference date of the ABPE, where by activity we mean an individual interacting with an administrative system (for example, when paying tax or changing address)

• appearance and activity on a single data source, with data linkage only used to deduplicate records that appear on more than one source

More details about the choice of data sources and the criteria for inclusion in the new ABPE method can be found in the Principles of ABPE V3.0 methodology.

The new methodology has produced population estimates for 2011 and 2016, where the 2011 reference date is 27 March (Census date), and the 2016 reference date is 30 June (Mid-Year Estimates (MYEs) reference date).

The analysis presented in this paper provides an insight on the quality of the ABPE V3.0 using newly developed measures of statistical uncertainty. These will feed into the evaluation of the ABPE V3.0 and will inform the development of the next iteration.

The measures of statistical uncertainty described in this paper were developed as part of a wider Uncertainty Project that we are conducting in collaboration with the University of Southampton Statistical Sciences Research Institute. The project aims at providing users of our population and migration statistics with information about their quality. The project has been successfully applied in the context of mid-year population estimates and has more recently been applied to admin-based population estimates.

Here we compare the admin-based population estimates (ABPEs) for 2011 and 2016 with the published Office for National Statistics (ONS) population estimates for 2011 to 2016, at the local authority (LA) level. The latter include 2011 Census estimates and 2011 to 2016 mid-year population estimates (MYEs), together with the MYEs measures of statistical uncertainty. Details of the methods used to measure uncertainty in the MYEs are available in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016 and Guidance on interpreting the statistical measures of uncertainty in ONS local authority mid-year population estimates. They are also summarised in Annex A, for reference.

Statistical uncertainty in local authority MYEs, 2011 to 16

A major statistical concern with the design of the local authority mid-year population estimates (MYEs) is that their quality decreases with time following the census. Statistical uncertainty in local authority MYEs grows each year between 2011 and 2016. Table 1 confirms that in 2011 the mid-year estimate uncertainty intervals were at their narrowest, with 330 local authorities having 95% uncertainty intervals of less than 5% of their mean simulated mid-year estimate values.

Initially most uncertainty comes from the census, but each year more uncertainty comes from internal and international migration. In 2012, for most local authorities (330 out of 348), the greatest proportion of uncertainty came from the census (see Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016, Section 6). The influence of the census declines over time. By 2016, census accounted for 50% of uncertainty in 155 local authorities.  The influence of international and internal migration becomes more visible.  In 2016, international migration accounted for more than 50% of uncertainty in 93 local authorities, while internal migration accounted for over 50% in just 17 local authorities.

Over time, a growing number of local authority mid-year estimates fall outside of their uncertainty bounds (Table 2). By 2016, over a third of local authority mid-year estimates do. This is consistent with our understanding that estimation of the population becomes progressively more difficult as we move away from the census. However, it could possibly be an artefact of the methodology for measuring uncertainty in the internal migration component of the MYEs, where the 2011 Census internal migration transitions are used as a benchmark of the "true" measure of internal migration (see  Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016, Section 5).

What does MYE uncertainty tell us about the local area level ABPEs?

In line with the design objective of undercounting the population, the ABPEs tend to fall below the MYE uncertainty intervals. Table 3 shows that in 2011, 290 (83%) of ABPEs fell below the MYE uncertainty interval. However, nine (2.6%) are above it. The MYE uncertainty bounds are designed to capture 95% of the simulated MYEs. Thus 2.5% of simulated MYEs fall on either side of the uncertainty bounds. Finding 2.6% of ABPEs above the MYE uncertainty bounds would be a welcome finding, except that ABPE V3.0 is designed to deliberately undercount the population.

Table 3 also shows that the ABPEs appear to align more closely with the MYEs in 2016 than they did in 2011. In 2011, only 14% of ABPEs fell within the MYE uncertainty bounds. By 2016 this rises to 45%. We know that MYEs have increasing bias through the decade after census. If we assume that the accuracy of the ABPE is stable over time, this would imply that MYEs are increasingly underestimating the population. Further research should investigate the relationship between the ABPEs and the true population count through time. This reinforces an important message in Developing our approach for producing admin-based population estimates, subnational analysis: 2011.

A listing of the local authorities in each cell of Table 3 is given in Annex B. Two illustrative examples are presented in Figures 1a and 1b.

We have produced indicative measures of statistical uncertainty for the 2011 admin-based population estimates (ABPEs). These are interim measures; ultimately confidence intervals will be generated as part of the ABPEs coverage assessment process.¹

Methodology for measuring statistical uncertainty in the ABPEs

Our approach relies on two simplifying assumptions. First, that we can use the variability between the ABPE and census estimates within groups of ”similar” local authorities as a proxy for variability of the ABPEs within those local authorities. The grouping of “similar” local authorities is achieved with reference to their patterns of comparability between the ABPEs and census by sex and single year of age. Second, that we can use 2011 Census estimates to represent the true population. Thus, our method doesn’t consider uncertainty in the 2011 Census estimates.

A full account of our methodology is provided in Indicative uncertainty intervals for the admin-based population estimates: July 2020. It can be summarised by the following process:

• calculate scaling factors comparing ABPE and Census by sex and single year of age for each local authority

• normalise the scaling factors around zero using the logarithmic transformation

• cluster local authorities based on similar patterns of logged scaling factors across age, for each sex separately

• for each cluster, fit a Generalised Additive Model through the lsf, to obtain the model residuals (error), r_i,j,k

• for each year of age and sex within a cluster, treat as a “group” and produce standardised residuals (s) by dividing them by their group’s standard deviation

• resample 1,000 standardised residuals (with replacement each time)
• un-standardise the residuals by multiplying by their group’s standard deviation
• add the residuals to the observed lsfs in each group to create 1,000 simulated lsfs
• exponentiate the simulated lsfs and multiply them by the published ABPE
• the uncertainty interval is taken as the 2.5th and 97.5th percentile of the 1,000 simulated population estimates

A small number of local authorities could not be clustered with others as they had distinct and unique scaling factor profiles. In these local authorities, the ABPEs often perform less well than in the others, for example, because the administrative sources don’t include foreign armed forces and their dependents. These “outlier” local authorities were grouped within their own separate clusters (separately for males and females) and, appropriately, have larger uncertainty intervals as a result. The outlier local authorities for males were Isles of Scilly, City of London, Forest Heath, Kensington and Chelsea and Rutland. For females the outliers were Isles of Scilly, City of London, Kensington and Chelsea, Forest Heath and Westminster. For further discussion about areas with large populations of armed forces (for example Forest Heath and Rutland) and the quality of the associated ABPEs see also Developing our approach for producing admin-based population estimates, subnational analysis: 2011.

2011 ABPE uncertainty by single year of age, sex and local authority

If the assumptions we have made in estimating uncertainty are correct, we would expect these intervals on average to capture the true population 95% of the time. Uncertainty interval widths for the ABPE reflect known patterns of statistical uncertainty in particular age-sex groups and are calculated as a percentage of ABPE. The intervals are on average wider at student ages and up to age 40 years, just before the retirement age and in the oldest ages. Figure 2 shows the average relative interval widths by age for males. The patterns are nearly identical for females.

In this section we report on the position of the 2011 ABPE relative to their uncertainty intervals.

Local authorities where the ABPEs sit entirely within their uncertainty bounds are not excessively biased at any point in the age distribution. For example, Figure 3 for Newport males. Few local authorities have ABPEs which sit within their uncertainty bounds for all ages; six for males (Kensington and Chelsea, Leeds, Newport, Rutland, Sunderland, Wirral) and two for females (Kensington and Chelsea, Westminster). In Westminster (females) and both males and females in Kensington and Chelsea, uncertainty intervals are especially wide (see Figure 4 for Kensington and Chelsea females).

Local authorities where the ABPEs are above their uncertainty bounds may be over-estimating the population at those ages. This typically occurs between ages 6 and 24 years, or around the pension age, and is equally common for males (193 local authorities) and females (191). This happens in five scenarios.

Scenario one

Most commonly, primary age children of both sexes (up to 11) may be being over-estimated. This affects most London boroughs, many urban boroughs in the North, a substantial number of urban and suburban local authorities and a few rural local authorities (see Annex C). 138 local authorities have at least one instance of overcount for boys up to 11 years, compared with 121 for girls. Females in the London Borough of Ealing is an example of potential primary age overcount (Figure 5).

Scenario two

In some local authorities ABPEs are above their uncertainty bounds in adolescent years (ages 11 to 17 years). This occurs for girls in 57 local authorities and for boys in 45, again listed in Annex C. Males in the London Borough of Wandsworth are an example (Figure 6).

Scenario three

Some local authorities (listed in Annex C) have ABPEs above the uncertainty intervals at ages 21 to 27 years (39 for females, 10 for males). These tend to have large student populations aged 18 to 21 years, and much smaller populations above undergraduate age. In these areas the ABPE may overcount students whose registration has remained after they have moved out and are no longer students there.

Scenario four

Three local authorities have ABPEs above the uncertainty interval at some other ages. City of London (28 to 37 years), Isles of Scilly (16 to 18 years, 28 to 30 years) and Boston (2 to 17 years, 22 to 38 years). Boston has a very high number of seasonal workers from Eastern Europe (Figure 7).

Scenario five

There are 162 local authorities where there is at least one instance of potential ABPE overcount for age 55 years or older; 108 for females and 116 for males. Table 4 shows local authorities with the highest frequencies.

Where ABPEs are above their uncertainty interval:

• occurs more frequently in urban local authorities, particularly London

• occurs most frequently at primary school age, student age (especially females) and post-retirement age

• for both males and females there is an increase in the number of local authorities with overcount from retirement age onwards; for females there is an additional increase in cases at 90 years old and above

• does not consistently increase by age at high ages

Most local authorities where the ABPEs are below their uncertainty bounds are meeting ABPE design objectives.There are just 11 local authorities where ABPEs do not fall below the uncertainty bounds at any age for males, and eight for females. 

ABPEs below the 95% uncertainty interval are concentrated between the ages of 18 to 26 years and 40 to 60 years and are more common and pronounced for males. Table 5 lists local authorities with the highest frequency of undercount, alongside the average percentage by which the ABPE is below the lower bound of the uncertainty interval. Males have more potential for undercount than for females, previously attributed in our 2019 publication to shortfalls in coverage of men in the contributing administrative sources. In some areas this may reflect the presence of Foreign Armed Forces or prisons (see also Developing our approach for producing admin-based population estimates, subnational analysis: 2011). Figures 8 and 9 show Camden females and Tunbridge Wells males.

Local authorities with differences between the ABPEs and the lower uncertainty bound at ages 18 to 26 years fall into three types.

Those with large student populations

The ABPE spike in the number of 18- to 21-year-olds present is lower than suggested by the 2011 Census and uncertainty bounds. Differences are typically greater for males. Males in Newcastle under Lyme (Figure 10) and females in Bristol (Figure 11) are examples.

Those with high student out-migration

Most local authorities (244) show a distinct drop in 18- to 21-year-olds, suggesting moves for higher education, or work. In some the decrease is much higher in the ABPEs than in the 2011 Census and implied by the uncertainty bounds. For males, 126 local authorities have ABPEs that are on average lower than the lower uncertainty bound. In 53 (listed in Table 6), the ABPE is more than 5% lower. In four, it is more than 15% lower (listed in Table 6). These patterns typically occur in rural areas and appear to be concentrated around wealthier rural or suburban areas (see Shropshire, Figure 12).

Other specific contexts

In a small number of local authorities, the ABPE underestimates young men in rural areas with an army base. In the London boroughs the ABPE appears to underestimate the number of 18- to 30-year olds (listed in Table 7).

Local authorities with substantial differences between the ABPEs and the lower uncertainty bound for 30- to 60-year-olds are mostly in the South, particularly the Home Counties. Demographically, these also fall into two types.

Rural or semi-urban areas

Rural or semi-urban areas with low numbers of 18- to 22-year-olds, together with a large number of 40- to 55-year-olds. ABPEs outside of the uncertainty bounds tend to be concentrated around ages 40 to 60 years. For females, 173 local authorities had ABPEs below the lower uncertainty bound for at least 15 ages in this age range. For males this was 168. There are a few local authorities with a gap between the lower uncertainty interval and the ABPE, but where there are also high numbers of 18- to 22-year-olds. This happens when a local authority encompasses a university town and a large surrounding rural area.

London boroughs

London boroughs where the ABPEs fall below the lower uncertainty bound at ages 30 to 45 years are listed in Table 8. Typically, these areas have large populations aged in their 30s. It is unclear why London suburbs are much more affected by this compared with suburbs of other cities.

After age 65 years, the number of local authorities with any undercount decreases, from roughly 400 observations of undercount at each age for both sexes leading up to age 65 years, to around 20 for each age after 65 years.

To conclude this section, what if our central assumption that we can use variability between the ABPEs and census within groups of “similar” local authorities as a proxy for variability of the ABPEs within those local authorities, is wrong? We also assume that the census represents the “true” population, with no account taken of uncertainty around the census estimates themselves. We tested our findings by comparing ABPEs against census estimates at single year of age with their associated uncertainty bounds. The methods are shown in Annex D. The results from this analysis reinforce all the findings within this section.

Notes for: What can we learn from statistical uncertainty in the ABPEs?

1. We acknowledge that there are minor differences in the 2011 ABPE data for 0-years old that we used for the analysis in Sections 6 to 7 of this paper and those that were used in Developing our approach for producing admin-based population estimates, subnational analysis: 2011 and Measuring and adjusting for coverage patterns in the admin-based population estimates, England and Wales: 2011. This reflects that when we started this work, we had an earlier extract of the data. The differences do not impact the uncertainty measures or any substantive points in the report.

For this comparison we first take mid-year population estimates (MYE) local authority-level uncertainty and produce uncertainty by single year of age. We then compare the ABPE single year of age uncertainty for males and females with those for the MYEs.¹

Methodology for measuring statistical uncertainty for local authority mid-year estimates by single year of age and sex

Annex A provides the methodology for estimating statistical uncertainty for MYE at local authority level. The method for breaking the local authority uncertainty down by single year of age and sex is summarised here and described more fully in Methodology for creating uncertainty intervals for the mid-year population estimates by single year of age and sex.

For the census base, we used the published five-year age group standard deviations as described in Annex D to generate 1,000 simulated estimates by single year of age, sex and local authority.

The internal migration in-flows and out-flows are already calculated for single years of age and sex.

For international migration in-flows, we mirrored the methodology that the Population Estimates Unit uses to calculate the international migration in-flow estimates by age and sex. First, 2011 Census data are used to cluster local authorities with similar age and sex profiles. Sex and age within the international in-migration component for each local authority are attributed based on the mean distributions within the cluster that the local authority has been assigned to.

For international migration out-flows, again we mirror Population Estimates Unit processes. First, the 2011 Census is used to cluster local authorities based on sex, age and citizenship (British, non-British). Within each cluster, we use the International Passenger Survey (IPS) data to create age, sex and citizenship (British, non-British) distributions. British and non-British emigrants are assumed to have different age structures. Three years of IPS data (current and two previous years) provide a smoothed (centred average) single year of age distribution by sex and citizenship for each cluster. Sex and age are then attributed for each local authority's emigration simulations based on the distributions in the cluster that the local authority was assigned to.

Natural changes (births and deaths) and minor adjustments are already available by single year of age and sex.

Because we are working with single years of age, we take into account time and population ageing. The cohort component approach is used to create the mid-year estimates. In this method the population at time t for each local authority is estimated using the formula

where the time t is measured in calendar years. To calculate the mid-year estimate for the year following the census we set the base population^(t-1) equal to the census estimate plus a population adjustment to account for the period between the census (March 27) and the mid-year point (June 30).

To calculate uncertainty measures for MYE at local authority level by sex and single-year of age (SYOA), the equation must be modified in order to account for the year-on-year ageing of the population. For this, we add age x parameter into the equation.

For x=0, babies under one:

For x>0, ages 1 and over:

Statistical uncertainty for 2011 local authority mid-year estimates by single year of age and sex

Statistical uncertainty in the MYEs is at its lowest in 2011 and in all local authorities, across all ages, the 2011 MYEs lie inside their uncertainty bounds. The uncertainty intervals are relatively narrow (see What do the 2011 ABPE uncertainty intervals and MYE uncertainty intervals by single year of age and sex tell us about the ABPEs?). Uncertainty intervals are wider for student and working age groups in some local authorities, for example Cambridge, Oxford, Liverpool (Figure 13), Birmingham and Coventry. We typically see no difference by sex within a local authority.

Comparison between the 2011 ABPEs by single year of age and sex and the 2011 MYE uncertainty intervals

In line with the ABPE design objectives, ABPEs more often lie under the mid-year estimate uncertainty intervals (48%) than above them (16%) (Table 9). ABPEs lie below the MYE uncertainty interval more often for males (50% of all single years of age) than for females (45%).

In every local authority in England and Wales the ABPE falls outside of the mid-year estimate uncertainty interval, either above or below, at certain single years of age. For males, the number of single years of age falling outside varies between 22 in Newcastle upon Tyne (Figure 14a) and Southampton to 86 in Rutland (Figure 14b). For females, they vary between 17 in Liverpool (Figure 14c) and 81 in Three Rivers (Figure 14d).

Potential overcount: ABPE lying above the mid-year estimate uncertainty intervals

For males, only Brighton and Hove has no ABPEs above the mid-year estimate uncertainty intervals at any age. By contrast, Blackpool ABPEs are above the mid-year estimate uncertainty interval at 51 single years of age.

For females, all local authorities have at least one age at which the ABPE is above the mid-year estimate uncertainty interval. Kirklees, North East Lincolnshire and Doncaster have just one age where this occurs, while Boston has 50. On average across local authorities, the ABPE falls above the mid-year estimate uncertainty interval 15 times for females and 14 times for males.

For both males and females, ABPEs tend to be above mid-year estimate uncertainty intervals for under-ones, children aged 5 to 18 years and pensioners (see Figures 15a and 15b). For females, this also occurs at 20 to 30 years. In relation to pensioners, the higher estimates in the ABPEs may be explained by possible problems in enumeration of care homes in the 2011 Census, or by possible displacement of this age group between their new address (if they moved to care homes) and their previous address – for a more detailed discussion about this see Developing our approach for producing admin-based population estimates, subnational analysis: 2011.

Where ABPEs are above the MYE uncertainty interval for males, they are on average 3.4% higher than the MYE upper bound. For females they are 3.1% higher on average. In most local authorities the potential overcount implied by the MYE upper bound is less than 5% – this applies to 78% of affected years of age estimates for males and 82% for females (see Table 10).

Potential undercount: ABPE below mid-year estimate uncertainty interval

In more than 300 local authorities, ABPEs are lower than mid-year estimate uncertainty bounds at student ages for males, and for ages 50 to 60 years for females. For females, this also occurs for 19-year-olds in more than 250 local authorities. The ABPEs are often below mid-year estimate uncertainty for ages 30 to 60 years, and for ages 30 to 40 years, more often for males than for females (see Figures 16a and16b).

Where ABPEs are below the MYE lower bound, they are on average 6.1% lower for males and 4.6% lower for females. In most local authorities the potential undercount implied by the MYE lower bound is less than 5% – this applies to 50% of affected years of age estimates for males and 63% for females. For 32% of males and 29% of females the potential undercount is 5 to 10% (see Table 10).

What do the 2011 ABPE uncertainty intervals and MYE uncertainty intervals by single year of age and sex tell us about the ABPEs?

The single year of age by sex MYE uncertainty intervals are generally narrower than the corresponding ABPE uncertainty intervals in 2011, when MYE quality is at its highest in census year. This is the case for 95% of all single year of ages, across all local authorities and for both sexes. ABPE uncertainty intervals for single year of age and sex are on average 2.7 times wider than the equivalent mid-year estimate uncertainty intervals. The mean ratio of ABPE: MYE uncertainty intervals widths is larger for males (2.84) than for females (2.58). The ratio is largely consistent across all ages.

For 65% of all ages, ABPE uncertainty intervals entirely contain the mid-year estimate uncertainty intervals, implying that they are both capturing the same “truth”, by very different methods. This occurs more often for males (68%) than for females (62%).

Non-overlapping uncertainty intervals

Non-overlapping MYE and ABPE uncertainty intervals only occur in 3.4% (2,174 out of 63,245) single years of age across all local authorities and both sexes. However, there is at least one single year of age where the uncertainty intervals don’t overlap in most local authorities; 279 for males and 303 for females (out of 348). The non-overlapping uncertainty intervals occur more commonly for females than males (55% and 45%). They are more commonly below the MYE uncertainty bounds (66%) than above them (34%). Table 11 shows the local authorities with most non-overlapping uncertainty intervals for MYEs and ABPEs.

Non-overlapping uncertainty intervals are most common at retirement ages, in some part attributable to their narrowness for both ABPEs and MYEs at these ages. However, non-overlapping uncertainty intervals are also more common among women than among men at working ages (see Table 12).

Notes for: What can we learn from comparing 2011 ABPE and Mid-Year Estimates uncertainty intervals, by single year of age, sex and local authority?

1. We acknowledge that the uncertainty measures for 2011 MYEs by single year of age, sex and local authority presented in this paper are provisional and should be treated with caution. Final results for both 2011 and 2012 MYEs will be published separately.

Admin-based population estimates (ABPE) Version 3 (V3.0) had a specific objective to remove the population overcount seen in ABPE Version 2 (V2.0). The analysis in this paper shows that this objective has not been fully met. There were 38 local authorities with ABPEs above the mid-year population estimates (MYEs) and their uncertainty bounds in either 2011 or 2016 or in both years. Developing methods to avoid ABPE overcount requires further research (see Measuring and adjusting for coverage patterns in the admin-based population estimates, England and Wales: 2011).

At local authority level the relationship between the ABPEs and MYEs has shifted over time. While 5% of ABPEs (19 of 348) were higher than the MYEs in 2011, by 2016 this increases to 19% (67 of 348). We show that the percentage of local authority ABPEs falling below the MYE lower uncertainty bound fell from 83% to 46% between 2011 and 2016. We know that the inter-censal estimates suffer increasing bias over time, largely because of reliance on the International Passenger Survey for measuring international migration (see also Section 5). In addition, internal migration may not be accurately captured. The closer alignment of ABPEs and MYEs in 2016 could be a product of increasing bias in the MYEs. However, we cannot rely on the untested assumption that the relationship between the true population and the administrative sources is constant over time. This requires further research. Time series analysis of the ABPEs and of the administrative sources at aggregate level, prior to any record linkage, would help to signal any change in quality if trends in one source are not visible in others (see also Developing our approach for producing admin-based population estimates, subnational analysis: 2011).

More granular analysis by single year of age and sex reveals the minimum degree of potential overcount in the ABPEs. Measured across local authorities, on average 15 single year of age estimates for females and 14 for males were above the upper bound of the MYE uncertainty interval. Comparing the ABPE and MYE uncertainty intervals, these were found not to overlap for 3.4% of single year of age estimates. This implies that over 96% of ABPEs may capture the same “true” population estimate at single year of age and sex. This does not necessarily imply that they capture the same individuals, for example, see Measuring and adjusting for coverage patterns in the admin-based population estimates, England and Wales: 2011 for compensating over- and under-count errors when linked to the census.

ABPE overcount is concentrated among the under-ones, children aged 5 to 18 years and pensioners. Overcount for each of these age groups requires further investigation (for pensioners it is discussed in more detail in Developing our approach for producing admin-based population estimates, subnational analysis: 2011). Are the ABPEs including people who are not usual residents? Or are some records being double-counted? Or are both happening? The overcount raises questions about whether the “activities” detected in administrative data really signal usual residence, and whether inclusion rules around co-resident inactive records are maybe too relaxed? How much linkage error is attributable to poor date of birth capture in the respective sources? These findings and the questions that they raise are consistent with those in Measuring and adjusting for coverage patterns in the admin-based population estimates, England and Wales: 2011.

Potential undercount in the ABPEs is highest at student ages (18 to 22 years), particularly for males, then falls, then increases again through working ages. This is notoriously a challenging group to capture in population estimates. The pattern is uneven across local authorities with universities. Do we have all the administrative sources that we need for this age group? How far can this undercount be explained by the rules excluding co-resident inactive adult children? 2011 Census data could inform this. Are the high levels of undercount seen in some local authorities correctable through coverage adjustment, and if so, how wide would the associated confidence intervals be for these ages?

The coverage adjustment challenge is more complex at sub-national level than at the national level. This is true for census-based estimates as well, however, administrative data raise additional challenges. Differential time lags in the administrative sources confound record matching. For matched records, address conflicts place records in the wrong geography. Counting records in the wrong place represents overcount in that location, alongside, potentially, undercount somewhere else. The complexity of adjusting for this in estimation underlines the need for ABPE design and the estimation strategy to be closely interrelated.

Further development of the ABPEs would be supported by use of the Error Framework for Longitudinally Linked Administrative Sources.This would help to ensure that statistical error is optimised for the ABPEs all the way through the production process. For further discussion on this see Developing our approach for producing admin-based population estimates, subnational analysis: 2011.

Likewise, the Error Framework should be rigorously applied to the linked data that form the basis of the ABPEs. Again, this is to ensure that statistical error is optimised for the ABPEs.

Mid-year population estimates (MYEs) use a cohort component method. In brief, components of demographic change (natural change (births less deaths), net international migration and net internal migration) are added to the previous year’s aged-on population. As well as adding the net components of change, additional procedures account for special populations (for example, armed forces, school boarders, prisoners). Initial work (see Quality measures for population estimates) identified the census base, international migration and internal migration as having the greatest impact on uncertainty, and our measure of uncertainty is a composite of uncertainty associated with these three components only.

Uncertainty can arise from data sources or from the processes used to derive the MYEs. We use observed data and recreate the MYEs’ derivation processes for the three components 1,000 times to simulate a range of possible values that might occur. Differences in data sources and procedures for each component imply different methods to generate the simulated distributions (see Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016 for details).

The simulated distributions are combined with the other components of change (assumed to have zero error, including births, deaths, asylum seekers, armed forces and prisoners). The uncertainty generation process is summarised in Figure 17. As with the MYEs themselves, the simulated estimates are rolled forward annually through the ten-year inter-censal period. Thus, we include both uncertainty carried forward from previous years (including from the census estimates) and new uncertainty for the current year.

Empirical uncertainty intervals for each local authority are created by ranking the 1,000 simulated values and taking the 26th and 975th values as the lower and upper bounds respectively. As the observed MYE generally differs from the central or median of the simulations, this confidence interval is not centered about the MYE and in some extreme cases the MYE is outside the uncertainty bounds.

Further details of the methods used to measure uncertainty in the MYEs are available in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016 and Guidance on interpreting the statistical measures of uncertainty in ONS local authority mid-year population estimates.

Figure 17: The mid-year estimate cohort component method and statistical uncertainty

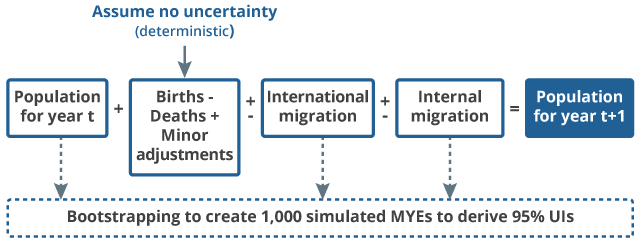
Source: Office for National Statistics

Download this image Figure 17: The mid-year estimate cohort component method and statistical uncertainty

.png (18.2 kB)

ABPE is within the MYE uncertainty interval in 2011 and 2016

Brent, Cambridge, Derby, East Lindsey, Great Yarmouth, Halton, Hartlepool, Hounslow, Hyndburn, Kingston upon Hull, City of, Leeds, Leicester, Lincoln, Luton, Newcastle upon Tyne, Newham, Newport, Norwich, Nottingham, Plymouth, Reading, Rhondda Cynon Taf, Southampton, Stoke-on-Trent, Sunderland, Tendring, Thanet, Torbay, Tower Hamlets, Waltham Forest

ABPE is within the MYE uncertainty interval in 2011 and below it in 2016

Bournemouth, Cardiff, Exeter, Liverpool, Preston, South Tyneside, Welwyn Hatfield

ABPE is within the MYE uncertainty interval in 2011 and above it in 2016

Barking and Dagenham, Burnley, Corby, Ealing, Haringey, Harlow, Northampton, Redcar and Cleveland, Sandwell, St. Helens, Tameside, Wellingborough

ABPE is below the MYE uncertainty interval in 2011 and below it in 2016

Adur, Amber Valley, Ashfield, Aylesbury Vale, Babergh, Bassetlaw, Bexley, Blaby, Blaenau Gwent, Bracknell Forest, Braintree, Bridgend, Brighton and Hove, Bristol, City of, Broadland, Bromley, Bromsgrove, Broxbourne, Caerphilly, Camden, Cannock Chase, Canterbury, Carmarthenshire, Central Bedfordshire UA, Ceredigion, Charnwood, Cheltenham, Chiltern, Chorley, Christchurch, Colchester, Conwy, Cornwall UA, Craven, Dacorum, Dartford, Daventry, Derbyshire Dales, Dover, Dudley, East Cambridgeshire, East Devon, East Hertfordshire, East Northamptonshire, Eastbourne, Eastleigh, Eden, Epsom and Ewell, Erewash, Fareham, Forest Heath, Fylde, Gateshead, Gedling, Gloucester, Gosport, Gravesham, Greenwich, Guildford, Gwynedd, Hackney, Hambleton, Hammersmith and Fulham, Harborough, Hastings, Havant, Havering, Herefordshire, County of, High Peak, Horsham, Huntingdonshire, Isle of Anglesey, Isle of Wight, Isles of Scilly UA, Kensington and Chelsea, King's Lynn and West Norfolk, Kingston upon Thames, Kirklees, Lewes, Lewisham, Lichfield, Maidstone, Maldon, Manchester, Medway, Melton, Mid Suffolk, Mid Sussex, Monmouthshire, New Forest, Newark and Sherwood, Newcastle-under-Lyme, North Dorset, North East Derbyshire, North Hertfordshire, North Lincolnshire, North Norfolk, North West Leicestershire, Northumberland UA, Pembrokeshire, Portsmouth, Powys, Reigate and Banstead, Richmond upon Thames, Richmondshire, Rochford, Rother, Runnymede, Rushcliffe, Rutland, Ryedale, Salford, Scarborough, Sevenoaks, Sheffield, Shepway, Shropshire UA, South Bucks, South Derbyshire, South Gloucestershire, South Lakeland, South Norfolk, South Northamptonshire, South Staffordshire, Southwark, St Edmundsbury, Stafford, Staffordshire Moorlands, Stockton-on-Tees, Swansea, Tandridge, Telford and Wrekin, Tewkesbury, Three Rivers, Tonbridge and Malling, Torridge, Tunbridge Wells, Uttlesford, Wandsworth, Waverley, Wealden, West Devon, West Dorset, West Lancashire, West Oxfordshire, West Somerset, Westminster, Wigan, Wiltshire UA, Windsor and Maidenhead, Worcester, Worthing, Wycombe, Wyre.

ABPE is below the MYE uncertainty interval in 2011 and within it in 2016

Allerdale, Arun, Ashford, Barnet, Barnsley, Basildon, Basingstoke and Deane, Bath and North East Somerset, Bedford, Birmingham, Bolsover, Bolton, Bradford, Breckland, Brentwood, Broxtowe, Bury, Calderdale, Carlisle, Castle Point, Chelmsford, Cheshire East, Chesterfield, Chichester, Copeland, Cotswold, County Durham UA, Crawley, Croydon, Darlington, Denbighshire, Doncaster, East Dorset, East Hampshire, East Riding of Yorkshire, Elmbridge, Epping Forest, Fenland, Flintshire, Forest of Dean, Harrogate, Hart, Hillingdon, Hinckley and Bosworth, Ipswich, Islington, Kettering, Lambeth, Malvern Hills, Mansfield, Mendip, Merthyr Tydfil, Mid Devon, Milton Keynes, Mole Valley, Neath Port Talbot, North Devon, North East Lincolnshire, North Kesteven, North Tyneside, North Warwickshire, Oadby and Wigston, Oldham, Poole, Purbeck, Redbridge, Redditch, Ribble Valley, Rochdale, Rossendale, Rugby, Rushmoor, Sedgemoor, Sefton, Selby, Slough, Solihull, South Cambridgeshire, South Hams, South Holland, South Kesteven, South Oxfordshire, South Ribble, South Somerset, Southend-on-Sea, Spelthorne, St Albans, Stevenage, Stockport, Stroud, Suffolk Coastal, Surrey Heath, Sutton, Swale, Tamworth, Taunton Deane, Test Valley, Thurrock, Torfaen, Trafford, Vale of Glamorgan, Vale of White Horse, Wakefield, Walsall, Warwick, Watford, Waveney, West Berkshire, West Lindsey, Weymouth and Portland, Winchester, Wirral, Woking, Wokingham, Wolverhampton, Wrexham, Wychavon, Wyre Forest, York.

ABPE is below the MYE uncertainty interval in 2011 and above it in 2016

Barrow-in-Furness, Blackburn with Darwen, Cherwell, Cheshire West and Chester UA, East Staffordshire, Enfield, Harrow, Hertsmere, Merton, North Somerset, Nuneaton and Bedworth, Pendle, Rotherham, Stratford-on-Avon, Swindon, Teignbridge, Warrington.

ABPE is above the MYE uncertainty interval in 2011 and above it in 2016

Blackpool, Knowsley, Peterborough

ABPE is above the MYE uncertainty interval in 2011 and within it in 2016

Boston, City of London, Coventry, Lancaster, Middlesbrough, Oxford

ABPE is above the MYE uncertainty interval in 2011 and below it in 2016

This does not occur.

Standard deviations for census estimates at single year of age are not available. We therefore assume that the coefficient of variation is the same for the single years of age as for the corresponding five-year age group. This allows us to estimate the standard deviation by single year of age¹:

Therefore

The 2011 Census estimates by single year of age, sex and local authority, and estimated standard deviation by single year of age, sex and local authority are used to specify the distribution (assumed to be normal) of uncertainty around the census component. Parametric bootstrapping from this normal distribution creates 1,000 simulations for the census component for each local authority by single year of age and sex.

Notes for: Annex D – Methodology for measuring 2011 Census uncertainty at single year of age

1. This approach is based on an analysis of five-year (published) and single-year (simulated) standard deviations from the 2011 Census, documented in minutes of the meeting between the University of Southampton Statistical Sciences Research Institute and Office for National Statistics on 25 July 2018.