Cynnwys
- Coronavirus (COVID-19) Infection Survey
- Study design: sampling
- Study design: data we collect
- Processing the data
- Test sensitivity and specificity
- Analysing the data
- Positivity rates
- Incidence
- Antibody and vaccination estimates
- Weighting
- Confidence intervals and credible intervals
- Statistical testing
- Geographic coverage
- Analysis feeding into the reproduction number
- Uncertainty in the data
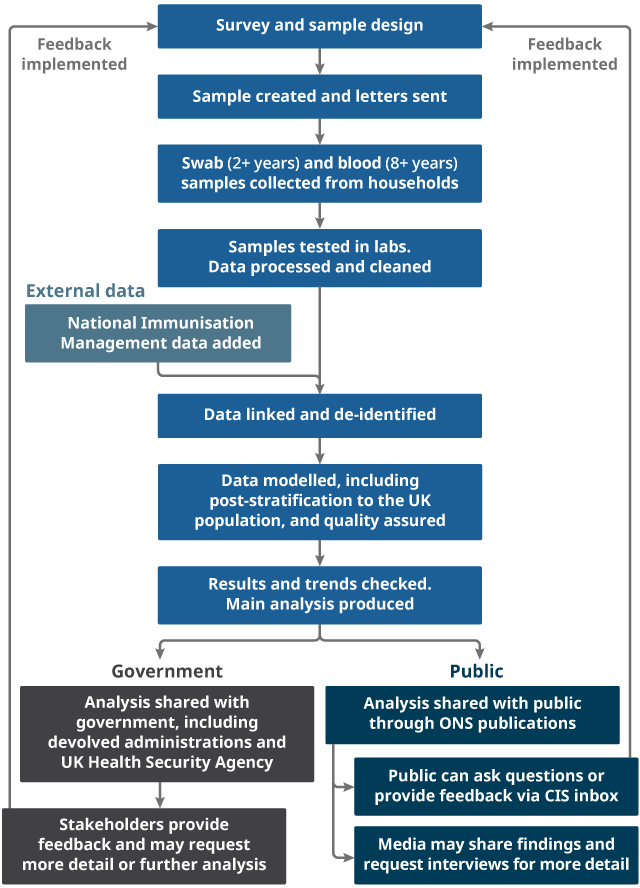
2. Study design: sampling
The sample for the survey in England, Wales, and Scotland is primarily drawn from AddressBase, a commercially available list of addresses maintained by Ordnance Survey. In Northern Ireland, the sample is selected by the Northern Ireland Statistics and Research Agency (NISRA) from people who have participated in NISRA and Office for National Statistics (ONS) surveys and have consented to be contacted again. This means that in all four countries only private households are included in the study. People living in care homes, other communal establishments and hospitals are not included.
We include children aged 2 years and over, adolescents and adults in the survey. Children are included because it is essential to understand the prevalence and the incidence of symptomatic and asymptomatic infection in those aged under 16 years. During some phases of the pandemic, this was particularly important for informing policy decisions around schools.
Initially, adults aged 16 years and over from around 20% of invited households were asked to provide a blood sample as well as a swab sample. To monitor the impact of vaccination on individual and community immunity and infection, this was increased. From February 2021, we asked adults from a larger but still representative sample of households in the study to give blood samples at their monthly visits.
Most of the sample (greater than 70%, but it varies by country) have been invited to give blood, and we collect up to 120,000 blood samples every month. To ensure we maintain this target, we send a small number of additional invites to give blood samples at regular intervals. Up until December 2021, we also asked all individuals from any household, where anyone had tested positive on a nose and throat swab, to give blood samples.
Blood samples are used to test for the presence of antibodies against SARS-CoV-2. Since 27 November 2021, children aged 8 to 15 years where at least one household member aged 16 years and over had already provided blood samples, were also asked to provide a blood sample.
The sample size has increased as the survey has expanded. At the start of the survey, in an initial pilot stage, we invited about 20,000 households in England to take part, anticipating that this would result in approximately 21,000 individuals from approximately 10,000 households participating. In the pilot stage, all invitations were sent to households where an individual was a current participant in the Labour Force Survey, or had previously participated in the Opinions and Lifestyle Survey and had agreed to be approached about future research. Both the Labour Force Survey and the Opinions and Lifestyle Survey are ONS social surveys. This meant the percentage of those approached who agreed to take part was higher than would normally be achieved from contacting a random sample of addresses. We initially took this approach to start getting information about COVID-19 positivity in the community as quickly as possible.
From August 2020, we expanded the survey by inviting a random sample of households from AddressBase. Fieldwork increased in England, and coverage of the study was extended to include Wales, Northern Ireland, and Scotland. Survey fieldwork in Wales began on 29 June 2020 and we started reporting headline figures for Wales on 7 August 2020. Survey fieldwork in Northern Ireland began on 26 July 2020 and we started reporting headline figures for Northern Ireland on 25 September 2020. Survey fieldwork in Scotland began on 21 September 2020 and we started reporting headline figures for Scotland on 23 October 2020.
From October 2020 to March 2022, the swab target was to achieve approximately 150,000 individuals with swab test results at least every fortnight in England, 9,000 in Wales, 5,000 in Northern Ireland, and 15,000 in Scotland (approximately 179,000 total across the UK). The blood sample target was to achieve up to 125,500 individuals with blood test results every month in England, 7,500 in Wales, 4,500 in Northern Ireland, and 12,500 in Scotland (approximately 150,000 in total across the UK). The absolute numbers reflect the relative size of the underlying populations.
From April 2022, a small number of existing participants were invited to move from study worker home visits to posted sample kits and completing questionnaires online or by telephone. This was to test the new ways of collecting data, swab samples and blood samples so that we could identify any issues and make adjustments before rolling out the new method to the rest of our participants. In line with this change, swab targets were reduced by around 25% to achieve up to 227,300 swab tests from individuals aged 2 years and over every 28 days in England, 15,650 in Wales, 10,050 in Northern Ireland, and 23,200 in Scotland (equating up to 276,200 swabs in total across the UK every 28 days, approximately 300,000 swabs in total across the UK per month).
The blood sample target was also reduced by around 20% (that is, retaining a greater percentage of those giving blood in order to maintain precision in monitoring declines in antibodies against SARS-CoV-2). Blood sample targets are now aimed to achieve up to 90,850 blood tests from individuals aged 8 years and over every 28 days in England, 6,300 in Wales, 4,150 in Northern Ireland, and 9,200 in Scotland (equating up to 110,500 blood samples in total across the UK every 28 days, approximately 120,000 in total across the UK per month).
More information about how participants are sampled can be found in the study protocol. We publish up-to-date information on sample size and response rates for all four countries in the Coronavirus (COVID-19) Infection Survey: technical dataset.
Remote data collection
In July 2022, we moved from collecting data and samples through home visits by a study worker, to a more flexible remote data collection method, with all questionnaires and swabs being completed remotely from the 1 August 2022. This was to ensure the survey remained as accessible and representative as possible for participants while moving to a more efficient method of data collection. Further information can be found in our blog post on the changes to remote data collection. Participants can now complete the survey online or by telephone, and swab and blood samples are returned through the post (or by courier for some participants). New data presented in the 19 August 2022 publication were based on a combination of data collected remotely and by study worker home visits. New data presented from the 26 August 2022 publication onwards were collected by remote data collection only.
In our Coronavirus (COVID-19) Infection Survey Quality Report: August 2022, we published findings from our initial pilot stage of remote data collection. These findings suggested that participants are satisfied with the new data collection method, with around 9 out of 10 participants indicating that they were either "satisfied" or "very satisfied". We also found minimal differences between estimates of swab positivity produced from remote data collection methods, compared with data collected by study worker home visits. In our Coronavirus (COVID-19) Infection Survey Quality Report: September 2022, we published findings on the likelihood of testing positive for antibodies against SARS-CoV-2 from our initial pilot stage of remote data collection. The results from this second quality report showed minimal differences between remote data collection and study worker home visit data collection.
Response rates
To achieve the required sample sizes, we invited a higher number of households to take part in the survey when sampling from address lists as opposed to households who agreed to be approached about other studies, as not everyone will choose to take part. Participants were offered the option to agree to follow-up visits when swabs and blood samples would be taken. Because of this, we expected a lower response compared with other surveys and therefore sent out a higher number of invites than the sample size required.
As likelihood of enrolment decreased over time since the original invitation letter was sent, response rate information for those initially asked to take part at the start of the survey in England were considered as final around six months after they received their invitation. Response rates for enrolment for data collection via study worker home visits ceased on 31 January 2022. On 26 September 2022, after the move to remote data collection, a small number of invitations to enrol in the survey were sent to a new sample of households in Northern Ireland. The latest response rates, along with commentary, are found in the Coronavirus (COVID-19) Infection Survey: technical dataset, Tables 2a to 2f.
Technical table 2a: UK
Provides a summary of the total number of households registered and eligible individuals in registered households for the UK.
Technical table 2b: England
Provides a summary of the response rates for England, by the different sampling phases of the survey:
- Table A presents response rates for those asked to take part at the start of the survey from 26 April 2020, sampled from previous ONS studies
- Table B presents response rates for those invited from 31 May 2020, sampled from previous ONS studies
Tables A and B can be considered as relatively final as the likelihood of enrolment decreases over time:
- Table C presents response rates for those invited from 13 July 2020, from a randomly sampled list of addresses
Technical table 2c: Wales
Provides a summary of the response rates for Wales by the different sampling phases of the survey:
- Table A presents response rates for those invited from 29 June 2020, sampled from previous ONS studies
- Table B presents those asked to take part from 5 October 2020, from a randomly sampled list of addresses
Technical table 2d: Northern Ireland
Provides a summary of the response rates for Northern Ireland for those invited from 26 July 2020 and from 26 September 2022, sampled from previous ONS and NISRA studies.
Technical table 2e: Scotland
Provides a summary of the response rates for Scotland for those invited from 14 September 2020, from a randomly sampled list of addresses.
Technical table 2f: swabs per day
Provides information on the number of swabs taken per day since the start of the survey from 26 April 2020.
Attrition
To produce reliable and accurate estimates, the survey sample should reflect the diversity of the population under investigation. Therefore, it is important we retain participants who agree to participate for the duration of the study. Some participants may not respond to the initial invite, withdraw their participation, or leave the study (for example, if they move house, as it is the physical address that is sampled in the survey design). If those who leave the sample are significantly different from those who remain, it may affect researchers’ ability to produce accurate estimates. We have to mitigate the risk of having a weekly sample that is not representative of the general population. To do so, we monitor attrition and change the sampling frequency across different households to improve the representativeness of each weekly sample.
We define attrition as participants who have formally withdrawn from the study for any reason. We calculate the attrition rate as the monthly count of formal withdrawals as a percentage of active participants for that month. These are defined as participants who have returned a swab or blood sample within the previous 90 days and have not withdrawn. Non-response from participants does not lead to being withdrawn automatically from the study, and therefore does not contribute to attrition rates. Monthly withdrawal data was not available prior to December 2020, and data are not presented by region, to reduce the risk of disclosing individuals. In August 2022, the study transitioned to a remote data collection method. This involves participants completing the survey online or by telephone, and returning swab and blood samples through the post (or by courier for some participants), as opposed to through study worker home visits. Data are therefore provided up to the end of July 2022.
In December 2020, 372,961 participants were actively participating in the study and 2,308 participants withdrew, resulting in an attrition rate of 0.62%. By October 2021, the number of active participants increased to its peak at 448,059, with an attrition rate of 0.58% for that month. By the end of July 2022, the number of active participants was 397,354 and 3,559 participants withdrew from the study, resulting in an attrition rate of 0.90%. Between December 2020 and the end of July 2022, attrition rates fluctuated, but peaked in June 2021 at 1.37% and were at their lowest in December 2021, at 0.32%. During this time, a total of 69,987 participants withdrew from the study.
The monthly number of active and withdrawn participants and attrition rates from December 2020 to July 2022 can be found in our Coronavirus (COVID-19) Infection Survey: attrition rates, UK dataset.
Nôl i'r tabl cynnwys3. Study design: data we collect
Nose and throat swab
We take nose and throat swabs to test for the presence of SARS-CoV-2, the virus that causes coronavirus (COVID-19). To do this, laboratories use a real-time reverse transcriptase polymerase chain reaction test (RT-PCR), not a lateral flow test.
We ask everyone aged 2 years and over in each household to take a nose and throat swab, regardless of whether anyone is reporting symptoms or not. Those aged 12 years and over take their own swabs using self-swabbing kits, and parents or carers use the same type of kits to take swabs from their children aged between 2 and 11 years. The survey was designed to find out more about how the virus is transmitted in individuals who test positive on nose and throat swabs; whether individuals who have had the virus can be reinfected; and about the incidence of new positive tests in individuals who have not been exposed to the virus before.
To address these questions, we collect data over time. Every participant is swabbed once; participants are also invited to have repeat tests every week for another four weeks; followed by monthly tests. Initially this was for a period of 12 months, but since March 2021 participants have been invited to remain in the study until 31 March 2023.
The protocol offers more detailed information about when and how we collect data. Information about how we process nose and throat swabs is found in Section 4: Processing the data.
Blood sample
We collect blood samples from a randomly selected subsample of participants aged 8 years and over to test for antibodies, which help us to assess the number of people who have been infected in the past, and the impact of the vaccination programme at both the population and the individual level. Participants give 0.5 millilitres of blood using a capillary finger prick method they do themselves. The blood samples are taken at enrolment and then every month.
The protocol offers more detailed information about when and how we collect data. Information about how we process the blood sample data is found in Section 4: Processing the data. Under the new remote data collection arrangements, participants send blood (and swab) samples to consolidation points via post or courier, where they are sent on to the University of Oxford laboratory. Residual blood samples are stored at the Biobank after testing, as long as consent is given for such storage. Blood samples are kept in a cool bag by study workers during the day, and then sent to the University of Oxford laboratory overnight.
Survey data
We use the Coronavirus (COVID-19) Infection Survey questionnaire to collect information from each participant, including those aged under 16 years. We collect information about their socio-demographic characteristics, any symptoms that they are experiencing, whether they are self-isolating, their occupation, how often they work from home, and whether the participant has come into contact with someone who has COVID-19. We also ask participants questions about their experiences of the pandemic, including questions about long COVID, whether participants have been vaccinated, how they travel to work, number of contacts with different amounts of physical and social distancing, and whether participants smoke.
From April 2020 to June 2022 across the UK, the questionnaire data were collected solely by a study worker during the visit to the participant(s). From July 2022, most participant data were collected through the new remote data collection arrangements, with all data being collected remotely from 1 August 2022.
Each participant in a household who agrees to participate is provided with an individual identifier. This allows for the differentiation of data collected between each household member.
Swabs and blood samples are labelled with a barcode, which is linked to the participant’s individual identifier on the study database.
Nôl i'r tabl cynnwys4. Processing the data
Nose and throat swabs
The nose and throat swabs are sent to the Lighthouse Laboratory in Glasgow. They are tested for SARS-CoV-2 using reverse transcriptase polymerase chain reaction (RT-PCR). This is an accredited test that is also used within the national testing programme. Swabs are discarded after testing. The virus genetic material from every positive swab with sufficient virus (cycle threshold (Ct) value less than 30) is sent for whole genome sequencing at the Wellcome Trust Sanger Institute, to find out more about the different types of virus and variants of virus circulating in the UK.
If a test is positive, the positive result is linked to the date that the swab was taken, not to the date that the swab was analysed in the laboratory.
The RT-PCR test looks for three genes present in coronavirus:
- N (nucleocapsid) protein
- S (spike) protein
- ORF1ab
Each swab can have one, two, or all three genes detected. The laboratory uses the Thermo Fisher TaqPath RT-PCR coronavirus (COVID-19) kit, analysed using UgenTec FastFinder 3.300.5, with an assay-specific algorithm and decision mechanism. This allows conversion of amplification assay raw data from the ABI 7500 Fast into test results with minimal manual intervention. Samples are called positive if at least a single N-gene and/or ORF1ab are detected (although S-gene Ct values are determined, S-gene detection alone is not considered sufficient to call a sample positive). We estimate a single Ct value as the arithmetic mean of Ct values for genes detected (Spearman correlation greater than 0.98 between each pair of Ct values). More information on how swabs are analysed can be found in the study protocol.
Recently, some of our swabs have been sent to the Rosalind Franklin and the Berkshire and Surrey Pathology Services laboratories for testing. This is to ensure resilience for testing capacity. We have investigated the potential effects of using multiple laboratories on our positivity results and, where necessary, have made minor statistical adjustments within our existing models to ensure consistency.
The Cycle threshold (Ct) value is the number of cycles that each polymerase chain reaction (PCR) test goes through before a positive result is detectable. If there is a high quantity of the virus present, a positive result will be identified after a low number of cycles. However, if there is only a small amount of the virus present, then it will take more cycles to detect it. These Ct values are a proxy for the quantity of the virus, also known as the viral load. The higher the viral load, the lower the Ct value. These values are helpful for monitoring transmission and for identifying patterns that could suggest changes in the way the virus is transmitting. We provide the Ct values of COVID-19 positive tests in the Coronavirus (COVID-19) Infection Survey: technical dataset. In some of our analysis, such as symptoms analysis, we define a “strong positive” as a swab with a Ct value of less than 30.
RT-PCR from nose and throat swabs may be falsely negative, because of their quality or the timing of collection. The virus in nose and throat secretions peak in the first week of symptoms but may decline below the limit of detection in people who present with symptoms or are tested beyond this time frame. For people who have been infected and then recovered, the RT-PCR technique provides no information about prior exposure or immunity. To address this, we also collect blood samples to test for antibodies.
Variants
We try to read all the letters of the virus’ genetic material for every positive nose and throat swab with sufficient virus to do so (Ct less than 30). This is called whole genome sequencing. Sequencing is not successful on all samples that we test, and sometimes only part of the genome is sequenced. This is especially so for higher Ct values up to 30, which are common in our data as we often catch people early or late in infection when viral loads tend to be lower (and hence Ct values are higher).
Where we successfully sequence over half of the genome, we use the sequence data to work out which type of variant is present in each virus. This method can tell us which variant might be responsible for any potential increase in cases, for example, cases which are either the Omicron variants or the Delta variant. However, because we cannot get a sequence from every positive result, there is more uncertainty in these estimates.
These data are provided in the Coronavirus (COVID-19) Infection Survey: technical dataset using the international standard labels.
The sequencing is currently produced by the Wellcome Trust Sanger Institute and analysis is produced by research partners at the University of Oxford. Of particular note are Dr Katrina Lythgoe, Dr Tanya Golubchik, and Dr Helen Fryer. Genome sequencing is funded by the COVID-19 Genomics UK (COG-UK) consortium. COG-UK is supported by funding from the Medical Research Council (MRC) part of UK Research and Innovation (UKRI), the National Institute of Health Research (NIHR), and Genome Research Limited operating as the Wellcome Trust Sanger Institute.
More information on the variants can be found in the Analysis of viral load and variants of COVID-19 section of our weekly bulletin, and information on how we measure the variants from positive tests on the survey can be found in our blog Understanding COVID-19 variants – What can the Coronavirus Infection Survey tell us?.
Blood samples to test for antibodies
Blood samples are tested for antibodies, which are produced to fight the virus. We use blood test results to identify individuals who have antibodies against SARS-CoV-2 at different levels which helps us understand the impact of vaccinations and COVID-19 infections, as well as possible levels of protection or vulnerability in different population groups over time.
It takes between two and three weeks after infection or vaccination for the body to make enough antibodies to fight the infection. Having antibodies can help to prevent individuals from getting infected again, or if they do get infected, they are less likely to have severe symptoms. Once infected or vaccinated, antibodies remain in the blood at low levels and can decline over time. The length of time antibodies remain at detectable levels in the blood is not fully known.
To test blood for antibodies, we use an ELISA for IgG immunoglobulins, based on tagged and purified recombinant SARS-CoV-2 trimeric spike (S) protein. Between March 2021 and January 2022, we also tested samples for IgG immunoglobulins against the nucleocapsid (N) protein to try to distinguish between those with immunity due to natural infection (who would be anti-S and anti-N positive) and vaccination (anti-S positive, but anti-N negative because vaccinations produce antibodies to the spike (S) protein only).
We use more than one level for antibody positivity analysis. The standard level for antibody positivity in the blood is 42 nanograms per millilitre (ng per ml), which corresponds to 23.5 binding antibody units (BAU) per ml using the World Health Organization’s (WHO) standardised units (enabling comparison across different antibody assays). This level was determined prior to the development of COVID-19 vaccinations and is CE marked by the Medicines and Healthcare products Regulatory Agency, providing 99% sensitivity and specificity in identifying unvaccinated people who have had a COVID-19 infection before (“natural immunity”) from unvaccinated people who have not.
However, research has shown that a higher antibody level provides a better measure of protection for those who have been vaccinated and not had a prior infection. Therefore, we introduced additional estimates of antibody positivity at higher levels.
In January 2022, a higher level of 179 ng per ml was introduced, which corresponds to 100 BAU per ml. This level was identified as providing a 67% lower risk of getting a new COVID-19 infection with the Delta variant after two vaccinations with either Pfizer or AstraZeneca vaccinations, compared with someone who was unvaccinated and had not had COVID-19 before. This higher level was identified by comparing how the risk of new COVID-19 infections with the most common COVID-19 variant at the time of the research, the Delta variant, varied across different antibody levels.
In May 2022, a higher level of 800 ng per ml was introduced, which corresponds to 447 BAU per ml. The 800 ng per ml level was chosen solely based on the test characteristics as the highest level that could be assessed since the start of antibody testing and is not based on any evidence on the level of antibodies needed for protection against the most dominant variant at the time – the Omicron variants, as this evidence was not available. Our latest antibodies results can be found in our Coronavirus (COVID-19) Infection Survey, antibody data, UK bulletin.
In October 2022, higher antibody levels were introduced to enable enhanced monitoring against antibody waning, at 2,000 ng per ml, 4,000 ng per ml and 6,000 ng per ml.
A negative test result will occur if there are no antibodies or if antibody levels are too low to reach the level being considered. It is important to draw the distinction between being estimated to have antibodies at different levels and having immunity meaning having a lower risk of getting infected or infected again.
Following infection or vaccination, antibody levels can vary and sometimes increase but are still below the level identified as “positive” in our test, and other tests. This does not mean that a person has no protection against COVID-19, as an immune response does not rely on the presence of antibodies alone. A person’s T cell response will provide protection but is not detected by blood tests for antibodies. A person’s immune response is affected by a number of factors, including health conditions and age. Additional information on the link between antibodies and immunity and the vaccination programme can be found in our blog What the ONS can tell you about the COVID-19 Vaccine programme.
The study protocol includes more information about swab and blood sample procedure and analysis.
Survey data
As in any survey, some data can be incorrect or missing. For example, participants sometimes misinterpret questions or may stop filling in the questionnaire part way through. To minimise the impact of incorrect or missing data, we clean the data, by editing or removing data that are clearly incorrect. For example, we correct the misspelled names of countries to which people say they have travelled.
Nôl i'r tabl cynnwys5. Test sensitivity and specificity
Understanding false-positive and false-negative results
The estimates provided in the Coronavirus (COVID-19) Infection Survey bulletin are for the percentage of the private-residential population that would have tested positive for COVID-19, otherwise known as the positivity rate. We do not report the prevalence rate. To calculate the prevalence rate, we would need an accurate understanding of the swab test's sensitivity (true-positive rate) and specificity (true-negative rate).
Our data and related studies provide an indication of what these are likely to be. To understand the potential impact, we have estimated what prevalence would be in two scenarios using different possible test sensitivity and specificity rates.
Test sensitivity
Test sensitivity measures how often the test correctly identifies those who have the virus, so a test with high sensitivity will not have many false-negative results. Studies suggest that sensitivity may be somewhere between 85% and 98%.
Our study involves participants self-swabbing, where there is the possibility that some participants may collect the swab sample incorrectly, which could lead to more false-negative results. However, since national testing programmes started in August 2020, most people in the UK became familiar with taking nose and throat swabs themselves.
Test specificity
Test specificity measures how often the test correctly identifies those who do not have the virus, so a test with high specificity will not have many false-positive results.
We know the specificity of our test must be very close to 100% as the low number of positive tests in our study over the summer of 2020 means that specificity would be very high even if all positives were false. For example, in the six-week period from 31 July to 10 September 2020, 159 of the 208,730 total samples tested positive. Even if all these positives were false, specificity would still be above 99.9%.
We know that the virus was still circulating at this time, so it is extremely unlikely that all these positives are false. However, it is important to consider whether many of the small number of positive tests we do have might be false. There are two main reasons we do not think that is the case.
Symptoms are an indication that someone has the virus; but are reported in a minority of participants at each visit. We might expect that false-positives would not report symptoms or might report fewer symptoms (because the positive is false). Overall, therefore, of the positives we find, we would expect to see most of the false-positives would occur among those not reporting symptoms. If that were the case, then risk factors would be more strongly associated with symptomatic infections than without reported symptoms infections. However, in our data the risk factors for testing positive are equally strong for both symptomatic and asymptomatic infections.
Assuming that false-positives do not report symptoms, but occur at a roughly similar rate over time, and that among true-positives the ratio with and without symptoms is approximately constant, then high rates of false-positives would mean that, the percentage of individuals not reporting symptoms among those testing positive would increase when the true prevalence is declining because the total prevalence is the sum of a constant rate of false-positives (all without symptoms) and a declining rate of true-positives (with a constant proportion with and without symptoms). However, this is not what our data shows.
More information on sensitivity and specificity is included in Community prevalence of SARS-CoV-2 in England: Results from the ONS Coronavirus Infection Survey Pilot by the Office for National Statistics' academic partners. You can find additional information on cycle thresholds in a paper written by our academic partners at the University of Oxford.
The impact on our estimates
We have used Bayesian analysis to calculate what prevalence would be in two different scenarios, one with medium test sensitivity and the other with low test sensitivity. Table 1 shows these results alongside the weighted estimate of the percentage testing positive in the period from 6 to 19 September 2020.
| Reference period: 6 to 19 September 2020 | 95% credible interval | ||
|---|---|---|---|
| Lower | Upper | ||
| Estimated average percentage of the population who had COVID-19 (weighted) | 0.2% | 0.2% | 0.3% |
| Prevalence rate percentage in Scenario 1 (medium sensitivity, high specificity) | 0.2% | 0.2% | 0.3% |
| Prevalence rate percentage in Scenario 2 (low sensitivity, high specificity) | 0.3% | 0.2% | 0.5% |
Download this table Table 1: The effects of test sensitivity on estimates
.xls .csvScenario 1 (medium sensitivity, high specificity)
Based on similar studies, the sensitivity of the test used is plausibly between 85% and 95% (with around 95% probability) and, as noted earlier, the specificity of the test is above 99.9%.
Scenario 2 (low sensitivity, high specificity)
To allow for the fact that individuals are self-swabbing, Scenario 2 assumes a lower overall sensitivity rate of on average 60% (or between 45% and 75% with 95% probability), incorporating the performance of both the test itself and the self-swabbing. This is lower than we expect the true value to be for overall performance but provides a lower bound.
The results show that when these estimated sensitivity and specificity rates are taken into account, the prevalence rate would be slightly higher but still very close to the main estimate presented in Section 2 of the Coronavirus (COVID-19) Infection Survey bulletin. This is the case even in Scenario 2, where we use a sensitivity estimate that is lower than we expect the true value to be. For Scenario 2, prevalence is higher because this scenario is based on an unlikely assumption that the test misses 40% of positive results. For this reason, we do not produce prevalence estimates for every analysis, but we will continue to monitor the impacts of sensitivity and specificity in future.
Evaluation of the test sensitivity and specificity of five immunoassays for SARS-CoV-2 serology, including the ELISA assay used in our study, has shown that this assay has sensitivity and specificity (95% confidence interval) of 99.1% (97.8 to 99.7%) and 99.0% (98.1 to 99.5%) respectively; compared with 98.1% (96.6 to 99.1%) and 99.9% (99.4 to 100%) respectively for the best performing commercial assay.
Nôl i'r tabl cynnwys6. Analysing the data
The primary objective of the study is to estimate the number of people in the population who would have tested positive for coronavirus (COVID-19) on nose and throat swabs, with and without symptoms.
The analysis of the data is a collaboration between the Office for National Statistics (ONS) and researchers from the University of Oxford and the University of Manchester. Our academic collaborators aim to publish an extended account of the modelling methodology outside the ONS bulletin publication in peer-reviewed articles, on topics including:
- vaccination effectiveness
- antibody waning and correlates of protection
- symptoms and SARS-CoV-2 positivity
- community prevalence of SARS-CoV-2 in England
- cycle threshold (Ct) values and positivity
- the Alpha variant, identified in the UK in mid-November 2020
- rates of seroconversion in NHS staff
- risks of coronavirus transmission from community household data (PDF, 681KB)
A full list of articles and academic papers by our academic collaborators can be found on the Nuffield Department of Medicine website.
All estimates presented in our bulletins are provisional results. As swabs are not necessarily analysed in date order by the laboratory, we will not have received test results for all swabs taken on the dates included in the most recent analysis. Estimates may therefore be revised as more test results are included.
Nôl i'r tabl cynnwys7. Positivity rates
We use several different modelling techniques to estimate the number of people who would have tested positive for SARS-CoV-2, the virus that causes coronavirus (COVID-19). As well as our headline figures, we provide estimates of the number of people who would have tested positive for infection broken down by different characteristics (age, region and so on). This section provides further information on our modelling techniques.
Bayesian multi-level regression poststratification (MRP) model
A Bayesian multi-level regression post-stratification (MRP) model is used to produce our headline estimates of positivity on nose and throat swabs for each UK country as well as our breakdowns of positivity by region and age group in England. This produces estimated daily rates of people who would have tested positive for COVID-19 controlling for a number of factors described in this section. Details about the methodology are also provided in the peer-reviewed paper from our academic collaborators published in the Lancet Public Health. Our code has also been made available in GitHub as part of a suite of public repository clones for users interested in replicating our analyses.
As the number of people testing positive (known as the positivity rate) is unlikely to follow a linear trend, time measured in days is included in the model using a non-linear function (thin-plate spline). Time trends are allowed to vary between regions by including an interaction between region and time. Given the low number of positive cases in the sample, the effect of time is not allowed to vary by other factors.
The models for the positivity rate for each country are run on the most recent seven weeks of data using all available swab data from participants from their respective country within time periods to estimate the number of people who are currently infected by COVID-19. We use a Bayesian multi-level generalised additive model with a complementary log-log link.
The Coronavirus (COVID-19) Infection Survey is based on a random sample of households to provide a nationally representative survey; however, some individuals in the original Office for National Statistics (ONS) survey samples will have dropped out and others will not have responded to the survey. To address this and reduce potential bias over time, the regression models adjust the survey results to be more representative of the overall population in terms of age, sex, and region, (region is only adjusted for in the England model). This is called “post-stratification”. The regression models do not adjust for ethnicity, household tenure or household size, because we do not have the underlying denominators across the UK for these characteristics. This is also true for deprivation and other similar measures, until these breakdowns using Census 2021 data are available. When they are available we will explore the feasibility of further post-stratification by deprivation, household size and urban/rural classification of the home address.
The data that are modelled are drawn from a sample, and so there is uncertainty around the estimates that the model produces. Because a Bayesian regression model is used, we present estimates along with credible intervals. These 95% credible intervals can be interpreted as there being a 95% probability that the true value being estimated lies within the credible interval. A wider interval indicates more uncertainty in the estimate.
We aim to provide the estimates of positivity rate that are most timely and most representative of each week. The most recent week of data reported is based on the availability of test results for visits that have already happened, accounting for the fact that swabs have to be couriered to the laboratory, tested and results returned.
On most occasions, the reference dates align perfectly between the four countries, but sometimes this is not feasible. Within the most recent week, we provide an official estimate for positivity rate based on a reference point from the modelled trends. For positivity rates, we can include all swab test results, even from the most recent visits. Therefore, although we are still expecting further swab test results from the laboratory, particularly for the most recent days, there are sufficient data for the official estimate for infection to be based on a reference point after the start of the reference week. To improve stability in our modelling while maintaining relative timeliness of our estimates, we report our official estimates based on the midpoint of the reference week.
Other models used for analytical purposes may use a different selection of variables. This decision is based on a judgement that takes into account what is being measured. For example, when we analyse which characteristics are associated with testing positive, we include a wider range of variables to identify which particular behaviours or characteristics are more likely to be associated with testing positive.
Sub-regional estimates
Sub-regional estimates were first presented for England on 20 November 2020 and for Wales, Northern Ireland, and Scotland on 19 February 2021. As sample sizes vary in local authorities, we pool local authorities together to create Coronavirus (COVID-19) Infection Survey sub-regions in Great Britain and we use Health and Social Care Trusts for Northern Ireland. Sub-regional estimates are obtained from a spatial-temporal Integrated Nested Laplace Approximation (INLA) model. This is similar to the dynamic Bayesian MRP model used for national and regional trend analysis that produces estimated daily rates of people who would have tested positive for COVID-19 controlling for age and sex within sub-regions. Spatial-temporal in this context means the model borrows strength geographically and over time, meaning that the model implicitly expects rates to be more similar in neighbouring areas, and within an area over time.
For our sub-regional analysis, we run a model for Great Britain and also separate models for Wales, Northern Ireland, and Scotland. This reflects the geography of the four countries as Northern Ireland does not share a land border with Great Britain; the geo-spatial model incorporates physical land distance between regions. Our academic partners from the University of Oxford have developed this spatiotemporal MRP methodology outside the ONS bulletin publication in a peer-reviewed article.
Initially for England, sub-regional estimates were produced using a six-day period. However, because of falling numbers of positive cases and smaller sample sizes in some sub-regions early in 2021, we changed to seven-day groupings to provide more accurate estimates for all countries of the UK; these were presented for the first time on 12 February 2021. To account for varying trends over time with greater precision, the length of the model was increased from 7 weeks to 13 weeks from 19 November 2021.
Sub-regional estimates are based on a different model to our headline estimates. As they are averaged over a seven-day period they should not be compared with our headline positivity estimates, which are for a single reference date. If a trend is changing quickly, our sub-regional estimates may not reflect the change we are seeing in our headline estimates.
In times of low prevalence, there are insufficient data to model at the subregional level and publication of these results will be paused.
Age analysis by category for England
We first presented our daily modelled estimates by age category for England on 11 September 2020 and refined our age categories on 2 October 2020. Our current age categories are:
- "age 2 years to school Year 6", which includes those children in primary school and below
- "school Year 7 to school Year 11", which includes those children in secondary school
- "school Year 12 to age 24 years", which includes those young adults who may be in further or higher education
- age 25 to 34 years
- age 35 to 49 years
- age 50 to 69 years
- age 70 years and over
Our current age categories separate children and young people by school age. This means that children aged 11 to 12 years have been split between the youngest age categories depending on whether they are in school Year 6 or 7 (birthday before or after 1 September). Similarly, children and young adults aged 16 to 17 years are split depending on whether they are in school Years 11 or 12 (birthday before or after 1 September). Splitting by school year rather than age at last birthday reflects a young person's peers and therefore more accurately reflects their activities both in and out of school.
The model used to produce our daily estimates by age category for England is similar to the model used to calculate our daily positivity estimates. We post-stratify the estimates so that results are adjusted to reflect the underlying population sizes.
We started publishing results from this updated model on 20 August 2021. Previously, the model presented the estimated level of infection using the East Midlands as a representative reference region. Therefore, previous results from our age category model are not comparable with national headline positivity estimates. The previous model also did not include the same interaction terms with time.
Methodology used to produce single year age over time estimates by UK country
To assess swab positivity over time by single year of age, we use frequentist generalised additive models (GAM) with a complementary loglog link and tensor product smooths between age and time. The latter allows us to incorporate smooth functions of age and time, where the effect of time is allowed to be different dependent on age. Tensor product smooths generally provide a better model fit than isotropic smooths when the covariates of a smooth are on different scales, for example, age in years and time in days.
The Restricted Maximum Likelihood (REML) method is used to optimise the smoothness of the curve given the observed data. The analyses are based on the most recent eight weeks of data on swab positivity among individuals aged 2 years and over. The effect of age and time are allowed to vary by region, but marginal probabilities and their confidence intervals are obtained for the whole of England. Separate models are run for England, Wales, Northern Ireland, and Scotland. In some instances, where REML over-smooths the fitted estimates, particularly when positivity rates are low overall or at some ages, we use a different estimation method called the Unbiased Risk Estimator (UBRE). This is most often applied to the devolved administrations but is not applied as a default.
Nôl i'r tabl cynnwys8. Incidence
The incidence of new PCR-positive cases (the number of new PCR-positives in a set period of time) helps us understand the rate at which infections are growing within the population and supports our main measure of positivity (how many people would have tested positive at any time, related to prevalence) to provide a fuller understanding of the coronavirus (COVID-19) pandemic.
The incidence rate is different to the R number, which is the average number of secondary infections produced by one infected person and was produced by the Scientific Pandemic Influenza Group on Modelling (SPI-M), a sub-group of the Scientific Advisory Group for Emergencies (SAGE), and subsequently by the UK Health Security Agency (UKHSA).
Current method for calculating incidence
We calculate the incidence of PCR-positive cases (related to the incidence of infection) from the Bayesian Multilevel Regression and Poststratification (MRP) model of positivity, using further detail from our sample. Because we test participants from a random sample of households every day, our estimate of positivity is unbiased providing we correct for potential non-representativeness owing to non-participation by post-stratifying for age, sex, and region.
We use information from people who ever test positive in our survey (from 1 September 2020) to estimate how long people test positive for. We estimate the time between the first positive test and the last time a participant would have tested positive (the “clearance” time) using a statistical model; more details on this follow. We do this accounting for different times between visits.
With these clearance time estimates we can then model backwards, deducing when new positives must have occurred in order to generate the positivity estimate. This method uses a deconvolution approach developed by Joshua Blake, Paul Birrell and Daniela De Angelis at the MRC Biostatistics Unit and Thomas House at the University of Manchester. Posterior samples from the MRP model over the last 100 days are used in this method.
Clearance time considers the sequence of positive and negative test results of an individual.
First, the clearance time for individuals testing negative, following a positive test, is modelled as occurring at some point between their last positive and first negative test.
Next, intermittent negatives within infection episodes as defined previously.
Next, a reinfection was identified in this analysis if any one of the following three conditions were met.
For time since previous infection and number of negative tests, if there is either:
- a positive test 120 days or more after an initial first positive test and following one or more negative tests
- a positive test 90 days or more after an initial first positive test and following two or more negative tests, or, for positive tests on or after 20 December 2021 when Omicron became the most dominant variant, following one or more negative tests
- a positive test 60 days or more after an initial first positive test and following three or more negative tests
- a positive test after an initial first positive test and following four or more negative tests
For high viral load:
- where both the first positive test and subsequent positive test have a high viral load, or there has been an increase in viral load between the first positive test and subsequent positive tests
For evidence of different variant types:
- where there is evidence, based on either genetic sequencing data or gene positivity from the polymerase chain reaction (PCR) swab test, that the variant differs between positive tests
The estimated distribution of clearance times is modelled using flexible parametric interval censored survival models, choosing the amount of flexibility in the model based on the Bayesian Information Criterion. We allow the distribution of clearance times to change according to the date a participant first tests positive. We also allow these distributions of clearance times to vary every 2 to 3 months to reflect changes in the pandemic, such as changes in COVID-19 variants that are dominant at that time.
There is a bias in estimating the clearance distribution because the analysis used to estimate how long a person stays positive only starts from their first positive test. Since (most) people will have become positive on an earlier day, this will bias the clearance curves downwards (making the estimates too short). However, there is another bias because of the survey missing positive episodes entirely if they are short. This means that our dataset has fewer short positive episodes than in the population as a whole, and that the sample used to run the analysis is biased towards people with longer positive episodes. This will bias the clearance curves upwards (making the estimates too long).
We tested whether the first positive a participant had in the survey was their first test in the study, and if not, how many days their last negative test was previously as explanatory variables. There was no evidence that either of these variables are associated with clearance time, and we have therefore used the overall estimate.
The estimate of the incidence of PCR-positive cases (relating to the incidence of infection) is produced by combining a posterior sample from the Bayesian MRP positivity model with the estimated distribution of the clearance times, allowing for the fact that some people will remain positive for shorter or longer times than others. Once the distribution of clearance is known, we compute a deterministic transformation (known as deconvolution) of the posterior of the positivity. The resulting sample gives the posterior distribution of the incidence of PCR-positive cases.
We calculate incidence estimates based on the MRP positivity model for the entire period of data in the MRP positivity model but we present it excluding the first two weeks. This is to avoid boundary effects (at the start of the positivity model, infections will have happened at various points in the past).
The official estimate of incidence is the estimate from this model at the reference date. The reference date used for our official estimates of incidence is 14 days before the end of the positivity reference day. This is necessary as estimates later than this date are more subject to change as we receive additional data. Where we have multiple positivity reference days for the four countries the earliest date is used.
This method of estimating incidence enables us to estimate incidence for Wales, Northern Ireland, and Scotland, as well as for England, as we can assume the same clearance distribution across all countries.
Nôl i'r tabl cynnwys9. Antibody and vaccination estimates
We present estimates of antibody positivity at different levels measured by antibodies to the spike (S) protein.
Current method for antibody and vaccination estimates
Modelled antibody and vaccination estimates use a spatial-temporal Integrated Nested Laplace Approximation (INLA) model with post-stratification. Post-stratification is a method to ensure the sample is representative of the population that can be used with modelled estimates to achieve the same objective as weighting. This estimation method is also used to produce sub-regional estimates for swab positivity and is like the multi-level regression model and post-stratification in the way that it uses Bayesian inference to derive an estimate. Spatial-temporal in this context means the model borrows strength geographically and over time.
For both antibody and previously presented vaccination estimates, we run two separate models: one for Great Britain and the other for Northern Ireland. This reflects the geography of the four countries as Northern Ireland does not share a land border with Great Britain; the geo-spatial model incorporates physical land distance between regions. All models are run on surveillance weeks (a standardised method of counting weeks from the first Monday of each calendar year to allow for the comparison of data year after year and across different data sources for epidemiological data).
From 29 November 2021, we started collecting blood samples from children aged 8 to 15 years. The age groups aged 8 to 11 years and aged 12 to 15 years are included in the Great Britain model.
The antibodies model for Great Britain adjusts for region or country and includes ethnicity, sex, and age groups (aged 8 to 11 years, aged 12 to 15 years, aged 16 to 24 years, aged 25 to 34 years, aged 35 to 49 years, aged 50 to 59 years, aged 60 to 64 years, aged 65 to 69 years, aged 70 to 74 years, aged 75 to 79 years and aged 80 years and over). The antibody model for Northern Ireland is a temporal model (no spatial component) because of lower sample size, and accounts for sex and age in wider groups (aged 16 to 24 years, aged 25 to 34 years, aged 35 to 49 years, aged 50 to 64 years, aged 65 to 74 years and aged 75 years and over).
From June 2021, we reduced potential bias in our antibody estimates by removing the participants from our analyses who had consented to antibody testing after being invited because an individual in the household had previously tested positive for COVID-19 on a nose and throat swab (under protocol 2.1). This had only a small impact on model estimates.
Our research partners at the University of Oxford have published several academic articles on antibodies against SARS-CoV-2 and vaccinations:
- Impact of Delta on viral burden and vaccine effectiveness
- Antibody response to SARS-CoV-2 vaccinations
- Impact of vaccination on new SARS-CoV-2 infections in the United Kingdom
- Total Effect Analysis of Vaccination on Household Transmission
- Anti-spike antibody response to natural SARS-CoV-2 infection in the general population
Method for producing estimates of antibody positivity over time by single year of age
To assess antibody positivity over time by single year of age (similar to single year of age swab positivity models) we used generalised additive models (GAM) with a complementary log-log link and tensor product smooths, with a spline over study day and age at visit. The analyses were based on the most recent eight weeks of data on antibody positivity among individuals aged 8 years and over. The number of participants aged over 85 years is relatively small so we recode these participants to be aged 85 years, which is a standard technique to reduce outlier influence. Separate models were run for England, Wales, Northern Ireland, and Scotland.
Antibody positivity estimates over time by single year of age have not been presented since 24 March 2022 (included data up to 6 March 2022) because antibody levels at the 179 nanograms per millilitre (ng per ml) level are consistently high (close to 100%) across age groups, so these statistics have become less useful. We continue to monitor antibodies to detect any new changes.
Vaccination estimates
To provide context for antibody estimates during the time when the vaccination programmes were progressing, we presented estimates of vaccination uptake in the population. Vaccination uptake was tracked over all visits over time. We validated our self-reported vaccination data in England with data from the National Immunisation Management Service (NIMS), which is the System of Record for the NHS coronavirus (COVID-19) vaccination programme in England. The equivalent of NIMS was not included for other countries, so vaccination estimates for Wales, Northern Ireland, and Scotland were produced only from Coronavirus (COVID-19) Infection Survey self-reported records of vaccination.
The vaccinations model for Great Britain was run at a subregional level and included ethnicity, vaccination priority age groups, and sex. The vaccination model for Northern Ireland was also run at a subregional level because of a higher number of participants with information about vaccination uptake. The model controlled for the effect of ethnicity by post-stratifying our analysis by the ethnic groupings of White and ethnic minorities (excluding White minorities), rather than individual ethnicities, because of sample size. The model accounted for sex and age in wider groups (aged 12 to 15 years, aged 16 to 24 years, aged 25 to 34 years, aged 35 to 49 years, aged 50 to 69 years, aged 70 years and over).
Vaccination estimates have not been presented since 23 February 2022 (including data up to 30 January 2022) because the national vaccination programmes were then well established and official administrative figures on vaccinations were published by the government. Our blog on vaccine effectiveness provides information on the effectiveness of vaccinations against the Alpha and Delta variants, which is based upon the research conducted by partners from the University of Oxford.
Nôl i'r tabl cynnwys10. Weighting
From May 2020, in addition to our post-stratified analyses described previously, we produced 14-day weighted estimates of the number of people who have coronavirus (COVID-19). These estimates were based on weighted data to ensure that they were representative of the target population in England, Wales, Northern Ireland, and Scotland. The study is based on a nationally representative survey sample; however, some individuals in the original Office for National Statistics (ONS) survey samples will have dropped out and others will not have responded to the study.
To address this and reduce potential bias, weighting was applied to ensure the responding sample is representative of the population in terms of age (grouped), sex, and region. This is different from the modelled estimates, which use a different method to adjust for potential non-representativeness of the sample through multi-level regression post-stratification (described in Section 7: Positivity rates).
Household size was initially included in the weighting but was dropped in October 2020 for three reasons:
to make the approach consistent with the model-based estimates (household size could not be used in the model)
because household size had a negligible impact on the estimates
because there were some concerns around measurement issues such as not having fully reliable population totals by household size available
We used to present weighted estimates for antibodies, but since 30 March 2021 have produced post-stratified modelled estimates.
The 14-day weighted estimates were helpful in the early stages of the pandemic as the modelled estimates were being developed. However, our modelled estimates provide the most accurate data on infection rates and are more easily able to show changes in trends. As a result, the 14-day weighted estimates for England by age group and regions of England have not been presented since 13 May 2022.
Confidence intervals for estimates
The statistics are based on a sample, and so there is uncertainty around the estimate. Confidence intervals are calculated so that if we were to repeat the survey many times on the same occasion and in the same conditions, in 95% of these surveys the true population value would fall within the 95% confidence intervals. Smaller intervals suggest greater certainty in the estimate, whereas wider intervals suggest uncertainty in the estimate.
Confidence intervals for weighted estimates were calculated using the Korn-Graubard method to take into account the expected small number of positive cases and the complex survey design. For unweighted estimates, we use the Clopper-Pearson method as the Korn-Graubard method is not appropriate for unweighted analysis.
Nôl i'r tabl cynnwys11. Confidence intervals and credible intervals
Simple explanations of confidence and credible intervals have been provided in previous sections, nevertheless, there is still some question about the difference between these two intervals. Whether we use credible or confidence intervals, depends upon the type of analysis that is conducted.
Earlier in the article, we mentioned the positivity model is a dynamic Bayesian multi-level regression post stratification model. This type of analysis produces credible intervals that are used to show uncertainty in parameter estimates, because this type of analysis directly estimates probabilities. While, for the single year of age over time estimates confidence intervals are provided because this is a different type of analysis using what are called frequentist methods. The use of confidence and credible intervals is a direct consequence of the type of statistics used to make sense of the data: Frequentist or Bayesian statistics respectively.
The difference between credible intervals and confidence intervals are associated with their statistical underpinnings; Bayesian statistics are associated with credible intervals, whereas confidence intervals are associated with frequentist (classical) statistics. Both intervals are related to uncertainty of the parameter estimate, however they differ in their interpretations.
With confidence intervals, the probability the population estimate lies between the upper and lower limits of the interval is based upon hypothetical repeats of the study. For instance, in 95 out of 100 studies, we would expect that the true population estimate would fall within the 95% confidence intervals. While the remaining five studies would deviate from the true population estimate. Here we assume the population estimate is fixed and any variation is because of differences within the sample in each study.
Credible intervals aim to estimate the population parameter from the data we have directly observed, instead of an infinite number of hypothetical samples. Credible intervals estimate the most likely values of the parameter of interest, given the evidence provided from our data. Here we assume the parameter estimates can vary based upon the knowledge and information we have at that moment. Essentially, given the data we have observed there is a 95% probability the population parameter falls within the interval. Therefore, difference between the two concepts is subtle: the confidence interval assumes the population parameter is fixed and the interval is uncertain. Whereas credible intervals assume the population parameter is uncertain and the interval is fixed.
Nôl i'r tabl cynnwys12. Statistical testing
Where we have completed analysis of the characteristics of people who have tested positive for coronavirus (COVID-19), we have used statistical testing to determine whether there was a significant difference in infection rates between different characteristics.
The test produces p-values, which provide the probability of observing a difference at least as extreme as the one that was estimated from the sample if there truly is no difference between the groups in the population. We used the conventional threshold of 0.05 to indicate evidence of genuine differences not compatible with chance, although the threshold of 0.05 is still marginal evidence. P-values of less than 0.001 and 0.01 and 0.05 are considered to provide relatively strong and moderate evidence of genuine difference between the groups being compared respectively.
Any estimate based on a random sample rather than an entire population contains some uncertainty. Given this, it is inevitable that sample-based estimates will occasionally suggest some evidence of difference when there is in fact no systematic difference between the corresponding values in the population as a whole. Such findings are known as “false discoveries”. If we were able to repeatedly draw different samples from the population for a characteristic where there is genuinely no association, then, for a single comparison, we would expect 5% of findings with a p-value below a threshold of 0.05 to be false discoveries. However, if multiple comparisons are conducted, as is the case in the analysis conducted within the Coronavirus (COVID-19) Infection Survey, then the probability of making at least one false discovery will be greater than 5%.
Multiplicity (the greater the number of tests, the greater the likelihood of a false discovery) can occur at different levels. For example, in the Coronavirus (COVID-19) Infection Survey we have:
- several different exposures of interest (for example, age and sex)
- several exposures with multiple different categories (for example, working location)
- repeated analysis over calendar time
Consequently, the p-values used in our analysis have not been adjusted to control either the familywise error rate (FWER, the probability of making at least one false discovery) or the false discovery rate (FDR, the expected proportion of discoveries that are false) at a particular level. Instead, we focus on presenting the data and interpreting results in the light of the strength of evidence that supports them.
Determining trends in our publications
In our weekly Coronavirus (COVID-19) Infection Survey bulletin, we usually comment on one-week or two-week trends in positivity estimates (for example, “the percentage of people who would have tested positive increased in the most recent week”). This commentary is informed by Bayesian probabilities of a change over the week or two weeks to the reference date. The probabilities return values between zero and 100, with probabilities below 10 or above 90 being a “very likely” decrease or increase respectively, and below 20 or above 80 being a “likely” decrease or increase.
It is also important to our users for us to say when trends are stable; that is, the estimates are not changing very much. To support this, we estimate the probability that the estimate on the reference date is more than 15% (relative) higher or lower, compared with one or two weeks previously. If the sum of the estimated probabilities is less than 20%, it is unlikely that the estimate has increased or decreased by a lot, and rates are therefore likely to be approximately stable.
Use of probabilities in commentary
Where there is strong evidence of a trend (“very likely increased” or “very likely decreased”) we say in commentary that rates have increased or decreased.
Where there are some signs of a trend, but the evidence is weaker (“likely increased” or “likely decreased”), we will usually only comment on a trend if it is sustained over a longer period. That is, the probabilities also implied an increase or decrease in the previous week’s data, or the increase or decrease is over both one and two weeks. This is to reduce the risk of highlighting trends that do not reflect genuine changes over time. Where we do comment on a new trend, we may say that there are “early signs” of an increase or decrease.
When positivity is low, uncertainty in modelled estimates is higher because the survey will identify few or no positives. In addition, where positivity rates are low, some users are more interested in whether rates remain below specified levels (we use 0.1% and 0.2%) than in the trend. Where positivity is consistently low, we therefore prefer to say positivity is “low” or “remains low”, showing that it is beneath 0.1% or 0.2% if appropriate, instead of commenting on a trend.
Nôl i'r tabl cynnwys13. Geographic coverage
Since 20 November 2020 for England, and since 19 February 2021 for Wales, Northern Ireland, and Scotland, we have presented modelled estimates for the most recent week of data at the sub-national level. To balance the granularity with the statistical power, we have grouped together groups of local authorities into Coronavirus (COVID-19) Infection Survey sub-regions. The geographies are a rule-based composition of local authorities, and local authorities with a population over 200,000 have been retained where possible.
For our Northern Ireland sub-regional estimates, our CIS sub-regions are NHS Health Trusts instead of groups of local authorities. The boundaries for these Coronavirus (COVID-19) Infection Survey sub-regions can be found on the Open Geography Portal.
Nôl i'r tabl cynnwys14. Analysis feeding into the reproduction number
The statistics produced by analysis of this survey contribute to modelling, which predicts the reproduction number (R) of the virus.
R is the average number of secondary infections produced by one infected person. The Scientific Pandemic Influenza Group on Modelling (SPI-M), a sub-group of the Scientific Advisory Group for Emergencies (SAGE), has built a consensus on the value of R based on expert scientific advice from multiple academic groups. This is now produced by the UK Health Security Agency (UKHSA).
Nôl i'r tabl cynnwys15. Uncertainty in the data
The estimates presented in this bulletin contain uncertainty. There are many sources of uncertainty, but the main sources in the information presented include each of the following.
Uncertainty in the test (false-positives, false-negatives and timing of the infection)
These results are directly from the test, and no test is perfect. There will be false-positives and false-negatives from the test, and false-negatives could also come from the fact that participants in this study are self-swabbing. More information about the potential impact of false-positives and false-negatives is provided in Section 5: Test sensitivity and specificity.
The data are based on a sample of people, so there is some uncertainty in the estimates
Any estimate based on a random sample contains some uncertainty. If we were to repeat the whole process many times, we would expect the true value to lie in the 95% confidence interval on 95% of occasions. A wider interval indicates more uncertainty in the estimate.
Quality of data collected in the questionnaire
As in any survey, some data can be incorrect or missing. For example, participants sometimes misinterpret questions or, in the case of remote data collection, may stop filling in the questionnaire part way through. To minimise the impact of this, we clean the data, editing or removing things that are clearly incorrect.
Nôl i'r tabl cynnwys