1. Introduction
This article presents the methodology used to calculate Consumer Prices Index including owner occupiers’ housing costs (CPIH)-consistent inflation rates for UK household groups. It is intended as a reference tool for anyone wanting to understand how the CPIH-consistent household group inflation rates are compiled.
The methodology presented in this article is largely unchanged from that published in 2017, relating to previous estimates of CPIH-consistent inflation rates for UK household groups published before May 2019. However, in the May 2019 publication, we introduced changes to the way we calculate imputed rents. We have therefore updated Section 4 and Annex A of this methodology article to include these changes.
This article is structured as follows:
- Section 2 introduces the theory behind constructing CPIH-consistent inflation rates for different household groups of the population, including a description of how a plutocratic and democratic-weighted CPIH can be calculated
- Section 3 describes the data sources required for this work
- Section 4 describes the methodology used to construct the CPIH-consistent inflation rates, including how estimates of imputed rents were constructed at a household level
- Section 5 concludes by describing some limitations to the existing methodology
It should be noted that these indices are experimental and therefore we would caution against any use of the indices, other than for research purposes. Where improvements are made to the methodology in future work, this article will be updated to reflect these changes. We welcome feedback on this methodology article to cpi@ons.gov.uk.
Nôl i'r tabl cynnwys2. Theory and notation
A price index has two basic components: data on the quantity of products purchased and information about the price of those products. In the UK, the Consumer Prices Index including owner occupiers’ housing costs (CPIH) uses a “Lowe” price index, which is a Laspeyres-type1 or fixed base weight index. This uses price-updated expenditure data from the weight reference period alongside information on prices in the current and base period, and is shown in equation [2.1a]:
Equation 2.1a
This can also be written as:
Equation 2.1b
In more simple terms, this formulation involves using changes in prices alongside expenditure weights from a fixed period. The prices of items that account for a larger (or smaller) fraction of expenditure in the reference period are given a greater (or lesser) weight in the calculation of the overall index.
By extension, the equivalent price index for any given household, h, is given by equation [2.2]:
Equation 2.2
Equations [2.1a] to [2.2] therefore set out the information that is needed to calculate price indices for both all households and an individual household. However, equation [2.2] also has the property that if it is weighted to reflect the spending of the relevant unit, the all-household price index can be recovered:
Equation 2.3
Equation [2.3] shows that the standard Laspeyres-type price index used in the CPIH weights the price experience of different households by their share of expenditure. Price indices of this form are described as having “plutocratic weights”. While this is not an explicit design of the methodology – which more heavily weights the prices of high-expenditure items – a secondary consequence of this approach is that households that spend more each period have a greater weight in the calculation of the CPIH than households who spend less. In effect, a household’s expenditure is weighted according to its position on the expenditure distribution2.
An alternative approach is a so-called “democratic” price index, where each household receives an “equal weight”, regardless of their level of expenditure. The index becomes:
Equation 2.4
To explore this further we consider the following alternative formation. To simplify the equations we have assumed that each expenditure value in this section will refer to expenditure in period r that has been price-updated to period 0. Consider a household’s budget share on item i:
Equation 2.5a
The democratic weight for item i is therefore equal to the arithmetic mean of the households’ budget shares for item i:
Equation 2.5b
With plutocratic weighting, each household budget share is weighted by their household expenditure eh = ∑i e h,i as a proportion of total whole-economy household expenditure E, where:
Equation 2.5c
The plutocratic weight for item i is therefore equal to:
Equation 2.5d
The US Bureau of Labor Statistics decompose this in a clear way:
“In the democratic index, the expenditure pattern of each household counts in equal measure in determining the population index; in essence, it is a case of ‘one household- one vote’. In the plutocratic case, the contribution of each household’s expenditure pattern is positively related to the total expenditure of that household relative to other households – in essence, ‘one dollar, one vote’”.
It follows that if all households have the same expenditure patterns and spend the same share of their expenditure on each good, then both formulas would give the same index.
Throughout this article and related literature, we refer to the different types of weighting as plutocratic and democratic3. The ONS working paper Investigating the impact of different weighting methods on CPIH presents a comparison of these approaches. Our related publication produces CPIH-consistent inflation rates for household groups using both plutocratic and democratic weighting.
Notes for: Theory and notation
- The CPIH is a Lowe index, in the sense that it uses current and previous period price information alongside expenditure weights that are price-updated. This feature distinguishes it from a Laspeyres price index, which uses current and previous period price information alongside observed, previous period expenditure weights.
- At What Price? (Schultze and Mackie, 2002) references calculations for the United States CPI that the household ‘represented’ by the plutocratic CPI is around the 75th percentile of the income distribution, which is closely mapped to the expenditure distribution. ONS (2014) concluded that the UK CPI is broadly representative of the price experience of households around two-thirds of the way up the expenditure distribution.
- It is noted that Astin and Leyland [Towards a Household Inflation Index, 2015] discourage the use of these names, however for consistency with previous literature, we remain with the convention of democratic and plutocratic weighting.
3. Data sources
As outlined in Section 2, the calculation of price indices requires two data inputs: quantities (or expenditure) and prices. This section sets out the data used to calculate Consumer Prices Index including owner occupiers’ housing costs (CPIH)-consistent inflation rates for UK household groups.
As household-level expenditure data for individual items can be volatile, this analysis uses expenditure and price data that are aggregated to the class-level categories defined in the Classification of Individual Consumption According to Purpose (COICOP). This is a slightly higher level of detail to that used in the CPIH, which includes a further “item level” in its classification structure, which is not defined in COICOP. Since March 2017, CPIH has also included an additional level of classification (level 5, or ECOICOP).
COICOP is a hierarchical classification system comprising: Divisions, for example, 01 Food and non-alcoholic beverages, Groups, for example, 01.1 Food, and Classes, for example, 01.1.1 Bread and cereals. As well as the 86 class-level categories identified in the COICOP structure, CPIH also includes an 87th category for Council Tax. While not part of the official UN COICOP structure, Council Tax is treated as a class-level category in the aggregation structure for CPIH.
CPIH is produced in stages, with indices derived at each stage weighted together to give higher level indices. The detailed input datasets that we use to construct the inflation rates for different household groups therefore provide information about how prices and expenditure have evolved for 87 categories of goods and services.
3.1 Price data
The CPIH is calculated from around 180,000 price quotes for around 700 goods and services each month. The price data that are used in this article are taken from the CPIH published class-level indices (available to a three decimal place level of accuracy). This ensures that errors arising from data aggregation are minimised.
However, the use of these data introduces the first of several limitations into our analysis. As shown in equation [2.2], the calculation of “true” household group-specific price indices requires the use of household-specific prices. However, as price data are collected from retailers rather than by asking households the prices they have paid for each item, separate price indices are not available for different types of household. As a result, this methodology assumes that households all experience the same changes in price. This limitation is discussed in greater detail in Section 5.
3.2 Expenditure data
The expenditure data used to calculate CPIH-consistent inflation rates for UK household groups come from several different sources. First, household-level expenditure data are taken from the Living Costs and Food Survey (LCF). The LCF is a continuous survey of the expenditure patterns of UK private households based on a sample of around 6,000 responding households per year. Demographic information about each household is also collected, along with the components required to calculate expenditure for each of the 87 class-level categories. The LCF contains the most detailed household-level expenditure data that is currently available to us.
For our publications, the LCF data we use for our analysis consist of around 6,000 households per year, surveyed between Quarter 1 (Jan to Mar) 2003 and Quarter 4 (Oct to Dec) of the most recent available year (for example, in 2019, we use data covering the period from 2003 to 2017).
An initial investigative analysis suggested that there were a small number of households whose expenditure we regarded as implausibly concentrated on a single product type and some that included negative expenditure (possibly reflecting the un-winding of prior overpayments). We therefore remove any households who report negative expenditure and households who spend 80% or more of their total expenditure on a single class-level category. This removes around 0.5% of the total sample and has no discernible impact on our results.
Our analysis also showed that there were observed households who reported very high total expenditure. However, as these are legitimate members of the sample and represent the very high expenditure households in the population, they are not excluded from this analysis.
In addition to micro-level data from the LCF, this method makes use of the aggregate household spending data that underpin the class-level weights and above used in the construction of CPIH, which are largely derived from System of National Accounts: SNA 2008 estimates of household final consumption expenditure (HHFCE). Using these data allows us to firstly replicate the CPIH directly and secondly calculate the difference between the published index and the price experience of households. These data were provided to us as annual expenditure totals for each of the 87 class-level categories.
Figure 1 shows a simplified process map for the calculation of CPIH weights for class-level and above. While the LCF weights – as published in the Family spending release – are an input for the HHFCE data and therefore for the majority of the CPIH weights, it is only one of a number of sources used to estimate household expenditure.
Alternative sources are used where the LCF is believed to under-report expenditure (including alcohol and tobacco) or where data quality is deemed to be stronger from administrative sources (including energy). Estimates also vary where the concepts captured in the national accounts differ from the pure expenditure estimates collected in the LCF. For example, the national accounts adjust the data to a domestic basis, while LCF only captures expenditure of UK private households (national basis). HHFCE is published quarterly in the Consumer trends release as part of the quarterly national accounts.
Figure 1: Sources of expenditure used in the CPIH weights (class level and above)
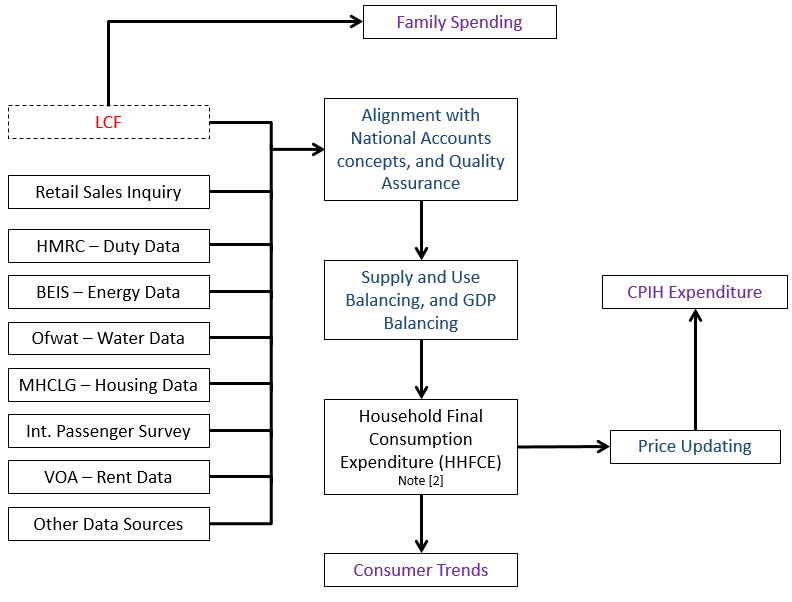
Source: Office for National Statistics
Notes:
- Figure shows a number of the sources and processes used in the compilation of the CPIH. LCF is the Living Costs and Food Survey, HMRC is Her Majesty’s Revenue and Customs, BEIS is the Department for Business, Energy and Industrial Strategy, Ofwat is the water regulator, MHCLG is the Ministry of Housing, Communities and Local Government, Int. Passenger Survey is the International Passenger Survey, VOA is the Valuation Office Agency.
- The weight for a small number of classes (for example, package holidays) uses a different source of information (see the Consumer Price Indices Technical Manual for more information).
Download this image Figure 1: Sources of expenditure used in the CPIH weights (class level and above)
.png (32.8 kB)The expenditure totals may also differ for reasons of data processing. Estimates of expenditure from the LCF used in the HHFCE may be affected by the supply and use, and GDP balancing processes before they are used to calculate the weights for CPIH. Timing is also an issue when using the LCF; to calculate new CPIH expenditure weights each year, observed expenditure from a previous year (the weight reference period) is “price updated” because expenditure data for the current year are not available. This involves taking the expenditure totals from the weight reference period and imputing their current value using the price change over the same period.
The lag in available expenditure data is why the CPIH uses a Lowe index (Section 2). It is a common approach across countries but results in differences between the CPIH and LCF estimates of household expenditure.
For the remainder of the article, we refer to the source used to calculate published CPIH as CPIH-consistent expenditure data and the survey data as LCF data.
Nôl i'r tabl cynnwys4. Methodology
This section details the methodology used to construct the Consumer Prices Index including owner occupiers’ housing costs (CPIH)-consistent inflation rates. It first describes how estimates of imputed rents were constructed at a household level. It then presents methods to align the Living Costs and Food Survey (LCF) microdata on household expenditure with CPIH-consistent total expenditure. The final step is to aggregate these CPIH-consistent expenditure weights for each household group together with prices to determine CPIH-consistent inflation rates for each household group.
4.1 Imputed rents methodology
The CPIH includes a measure of owner occupiers’ housing costs (OOH). These are the costs of housing services associated with owning, maintaining and living in one’s own home. To produce CPIH-consistent inflation rates for various household groups, it is therefore necessary to produce estimates of OOH at the individual household level.
CPIH uses an approach called rental equivalence to measure OOH. The rental equivalence approach assumes that a dwelling is a capital good and therefore is not consumed, but instead provides a flow of services that are consumed each period. It imputes owner occupiers’ housing costs from the rents paid for equivalent rented properties. This requires data on the housing costs of actual renters to estimate the price that owner occupiers would pay to consume the same level of housing services. This concept, known as “imputed rents”, captures the implied price change associated with owner occupation.
For the aggregate CPIH, the expenditure weight for imputed rents comes from the household final consumption expenditure (HHFCE). These are calculated by multiplying dwelling stock counts for the total owner occupied sector (from the Ministry of Housing, Communities and Local Government data) by average rental prices from Valuation Office Agency (VOA)1 data.
However, the MHCLG and VOA data used to calculate the aggregate CPIH expenditure do not have the information required to calculate estimates of imputed rents at the individual household level. As the LCF microdata used elsewhere in this methodology also includes information on the level of rent, any housing benefit received by households and the characteristics of the house and household, we can use this to create a model of imputed rents at the household level.
A summary of the imputed rents methodology follows (for more information, please see Annex A):
- obtain data on the level of rent paid by households with private, unfurnished and unsubsidised tenancies (other tenancy types are not used to calculate imputed rent; please refer to Annex A for further details) and the characteristics of both these rented properties and the households that rent them
- estimate a two-stage Heckman model, which explains rent paid as a function of the characteristics of the house rented and demographics of the household that live there, while partially accounting for selection into rented accommodation
- use the coefficients from this model to estimate the level of imputed rent for all owner occupiers identified in the LCF data
- calibrate these estimates with higher-level averages from the VOA data and merge these expenditure back into the main LCF dataset
Since the previous release, several methodological improvements have been implemented. These are summarised as follows (for more information, please see Annex A):
- one variable has been removed as an independent variable in the prediction model
- only renters with private, unfurnished and unsubsidised (that is, not supported in whole or in part by housing benefit) tenancies are considered “renters” for the purpose of calculating imputed rent for owner occupiers, as opposed to the previous method, which used all renters
- a bias correction term has been included in the Box-Cox back-transformation
- ordinary least squares (OLS) is now used to estimate the prediction model as opposed to weighted least squares (WLS)
The results of the imputed rents methodology are shown in Figure 2, which presents the distribution of actual rent and imputed rent (before and after calibration). Annex B presents this analysis on a regional basis.
The final step of calibrating to the VOA data spreads out the LCF estimates, resulting in a distribution of imputed rents that is similar to that of actual rent, with a small shift to the right. This means that average imputed expenditure for owner occupiers is slightly greater than average observed expenditure for households that rent.
This difference in average expenditure on rent is less pronounced than when calculated using the previous method, possibly reflecting the change in the definition of a “renter” from all renters to just those in private, unfurnished and unsubsidised tenancies (with those that are supported by housing benefit being removed from the definition). While the housing stock for renters is generally considered to be of lower quality than that for owner occupiers, the housing stock relating specifically to private, unfurnished and unsubsidised tenancies will likely be of a quality most similar to that of owner occupiers.
Figure 2: Distribution of actual rent and imputed rent on a Living Costs and Food and Valuation Office Agency basis, over the whole dataset
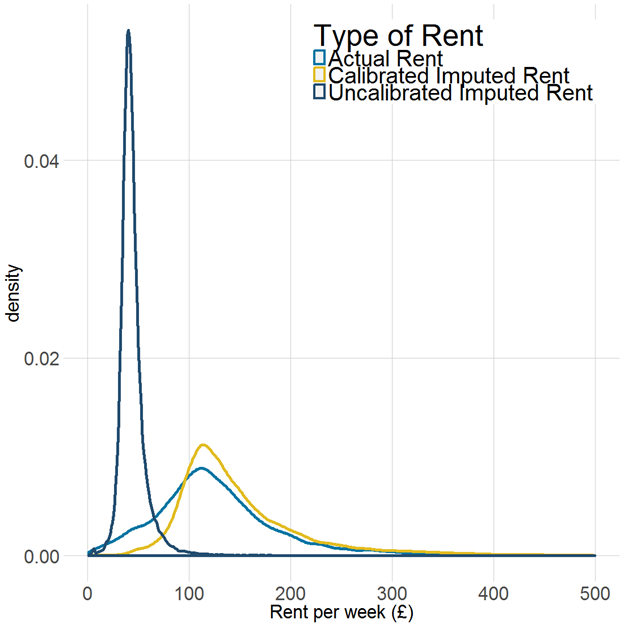
Source: Office for National Statistics
Notes:
- These charts are based on the underlying distribution of the data. The line is a continuous function (that is, it is created using a model to estimate the equation of the plotted line) and therefore there are no underlying data values that can be downloaded.
Download this image Figure 2: Distribution of actual rent and imputed rent on a Living Costs and Food and Valuation Office Agency basis, over the whole dataset
.png (58.2 kB)There are further developments to this model that could be investigated in future work. For example, improvements could be made to the selection stage of the model, which currently lacks an appropriate exclusion restriction (that is, a variable that influences the probability of renting, but not the level of rents). Consequently, the estimated coefficients in the current model are unlikely to have been completely purged of selection bias. In addition, the change in the definition of a “renter” means that variable selection for both stages of the Heckman model could be re-performed to reflect this change. Where improvements are made to the methodology in future work, this article will be updated to reflect these changes.
4.2 Aligning the LCF microdata with CPIH aggregate expenditure
Once the imputed rents expenditure estimates are calculated for each household, the expenditure for the remaining 86 class-level categories (Section 3) are calculated. The LCF uses the Classification of Individual Consumption According to Purpose (COICOP) coding frame for expenditure items and we can therefore map the lower level LCF expenditure categories to the class-level categories. The resulting dataset includes estimates of expenditure for each of the 87 class-level categories used in the CPIH aggregation, for each household.
These expenditure data are then price updated, following the same procedure to that used in the CPIH and then a redistribution process is undertaken, which ensures the total expenditure weights are consistent with the aggregate CPIH.
4.2.1 Price updating
Over the period 2005 to 2016, the CPIH aggregate class-level weights have been updated annually with a reference period of December of the previous year. They are based on the previous calendar year’s HHFCE data (Figure 1). For instance, for 2016, the weights reference period is December 2015, with the underlying expenditure data referring to the 2014 calendar year. The expenditure data are price updated at the level of COICOP class to the reference period using movements in the relevant class price index.
Since 2017, this methodology has changed slightly. Under the previous process, for 11 months of the year, the month to which weights are price-updated (December) and the price reference period (January) are different. For a Lowe price index (Section 2) these two periods should theoretically be the same. Therefore, in January, CPIH uses weights that have been price updated to December (as it does already), but from February to December, it uses weights that have been price updated to January. For more information about this change, please see Assessing the Impact of methodological improvements on the Consumer Prices Index.
For consistency, the same methodology is applied to the LCF microdata, which come from two years prior to the current year (consistent with the HHFCE data). For 2005 to 2016, weights are calculated using a single price update to December. For instance, for 2016, the underlying expenditure data refer to the 2014 calendar year and are price updated to reference period December 2015. This process takes the price index in December 2015 divided by the average price index in 2014 to create an “uprating factor”, which is then used to update the 2014 LCF microdata to 2016. We represent this as follows.
For a given year y in the period 2005 to 2016, the weights are based on LCF expenditure in year y-2. Our uprating factor for COICOP class i, Ui can be written as:
Equation 4.1
For 2017, and for the following years, weights for January are calculated using the same approach. For February to December, weights are calculated using a double update to January. For instance, for February to December 2017, the underlying expenditure data refer to the 2015 calendar year and are price updated to reference period January 2017.
Our double uprating factor for COICOP class i, UiD can be written as:
Equation 4.2
These uprating factors are then applied to the household level estimates of expenditure for each of the 87 class-level categories. For 2017, and for the following years, the LCF data is copied and the different uprating factors are applied to give a set of household expenditure that can be used for the January 2017 weights and a separate set of expenditure that can be used for February to December 2017.
It is important to note the assumption that price updating requires. When you price update, you assume the quantity doesn’t change but the price has. When you don’t price update, you assume the distribution of expenditure hasn’t changed. This will only affect our results if different household groups experience stronger or weaker substitution effects. Future work could be conducted to test this assumption using different vintages of LCF data.
4.2.2 Reconciling CPIH-consistent expenditure totals with the LCF microdata
In order to construct household-level expenditure estimates that aggregate to the CPIH expenditure weights, we effectively “allocate” the CPIH-consistent expenditure totals for each class across the observed LCF households based on their reported expenditure. This allows us to produce weights and indices for each household group that are consistent with published CPIH and make conclusions from the analysis on the basis of differences in methodology applied, rather than differences in underlying data.
There are several methods to do this, but following further testing and advice from our Technical Advisory Panel for Consumer Prices (APCP-T), the method chosen is the same approach used in a previous version of this work published in 2014. For this method, we divide reported total CPIH expenditure on each of the 87 COICOP classes among the households we observe in the LCF, in proportion to their expenditure share on that class-level category. These expenditure shares are calculated using weighted household spending from the LCF, which ensures that the total expenditure is representative of the population rather than just the LCF sample:
Equation 4.3
Equation [4.3] states that total CPIH-consistent spending on a given product is divided among the observed households in proportion to the share of total observed spending on that product reported in the LCF. Households that report more (or less) expenditure on a given product are awarded a greater (or lesser) fraction of total expenditure taken from the CPIH.
For instance, if an observed household accounts for 0.05% of total purchases of bread and cereal products in the LCF, it is allocated the same fraction of the CPIH expenditure total on bread and cereal. This requires an important assumption: that where there are differences between the LCF and CPIH-consistent expenditure totals for a given COICOP, these differences arise because all households over- or under-report their expenditure by the same proportion.
While this approach was deemed the most suitable during testing, there are still a number of issues that are caused by applying this methodology. For example, where the expenditure weight within the CPIH is based on data other than the LCF data, the differences between the CPIH-consistent and LCF expenditure totals can be extremely large. There are also some instances where the coverage of the LCF data is low and therefore a large amount of CPIH expenditure is allocated to a small number of households for a particular class. For example, medical and paramedic services are a COICOP class where a very small number of households reported spending over the full dataset.
In these cases, we adjust our methodology to avoid distorting the results:
- for each year, COICOP classes were identified where both these two conditions were met:
- the ratio of CPIH to LCF expenditure is greater than two (that is, total CPIH expenditure is more than double the LCF expenditure)
- the percentage of households that report spending on that COICOP class over the year is less than 20%
- spending on these COICOP classes is allocated using the reported proportion of household expenditure on a higher aggregate (group if available, or division level)
Using this methodology requires the assumption that it is suitable to allocate total spending on a COICOP class (6.3.1 Medical and paramedic services, for instance) using reported household expenditure on a higher aggregate – (6 Health, for instance). In other words, the proportion of total LCF expenditure that the household spends on the higher aggregate (6 Health) is then applied to the CPIH-consistent expenditure data for that class (6.3.1 Medical and paramedic services) [equation 4.4] (this is a modified version of equation 4.3):
Equation 4.4
This adjustment ensures that our methodology does not allocate very high levels of spending to a relatively small number of households, which in turn would distort the picture of household inflation.
As opposed to choosing a fixed set of COICOP classes for all years, the COICOP classes are identified on a yearly basis using the previous criteria and expenditure is allocated appropriately. This method is preferred to choosing a fixed set over a long time period, which may not reflect changes in data sources across years. This also means that this method is robust for future publications. Classes identified by these conditions generally account for 4% to 5% of the overall CPIH basket of goods and services.
Before deciding on this approach, various different conditions were identified and tested. It was found that modifying the classes used to reallocate the expenditure in this adjusted manner had minimal impact on the inflation rates experienced by different household groups and did not distort the overall trends.
4.3 Index aggregation
After these data processing steps, the final dataset consists of expenditure estimates for each household that are consistent with the CPIH class-level expenditure totals when aggregated over each year. The expenditure shares are then calculated for each household group, using either the plutocratic or democratic method of weighting. This gives a set of weights for each household group on a CPIH-consistent basis.
To calculate the inflation rates for each household group, unrounded class-level price indices for each month are taken from the CPIH and combined with the appropriate expenditure weights to produce an aggregate price index. The resulting indices are double chain-linked; first in January, which accounts for the annual changes in the COICOP weights for the class, group- and division-level products. A further chaining step, to account for changes in the basket of representative items – the goods and services that are aggregated up to form the class-level of CPIH – occurs in February.
For more information about how the CPIH is constructed, please see the Consumer Price Indices Technical Manual.
Notes for: Methodology
- We shall refer to this data as VOA data for brevity. It should be noted however that data from the VOA only covers England. Data for Scotland was obtained from the Scottish Government, for Wales from the Welsh Government and for Northern Ireland, from the Northern Ireland Housing Executive. This is because housing policy has been transferred to the devolved administrations and the data are therefore not collected by one governmental body.
5. Limitations
While the calculation of inflation rates for household groups is analytically straightforward, a range of data constraints make their estimation challenging in practice. This section discusses the limits of our analysis with the aim of transparency for users. Where improvements are made to the methodology in future work, this article will be updated to reflect these changes. These limitations do not impede the validity of the chosen methodology and its robustness.
5.1 Common price indices
One of the main limitations of this analysis is the use of national price indices alongside household group-specific expenditure weights. An analysis of household group-specific inflation rates would ideally use price indices and expenditure weights specific to each household. While the expenditure weights used here capture differences in the consumption patterns of different households, the lack of household group-specific price indices means that this method assumes that all households experience the same change in the prices that they pay.
While this may be a fair assumption for some items – TV licences for instance, for which there is little variation in price – it is less likely to hold in product categories that comprise large numbers of heterogeneous items – such as second-hand cars. In these categories, the products included in the Consumer Prices Index including owner occupiers’ housing costs (CPIH) are selected to be representative of the purchases of all households and therefore capture “average” price movements. As a result, they may be more or less representative of the price changes that different household groups experience.
The impact of this assumption on our analysis depends on the extent to which households experience different price changes for goods in the same Classification of Individual Consumption According to Purpose (COICOP) class. As data on the degree to which price changes vary for different types of household are not available, it is not possible to quantify this limitation with any precision. In future, alternative data sources may provide a more comprehensive source of information from which better estimates of how price changes differ for different groups of households can be derived.
5.2 Data sources
As already discussed in Sections 3 and 4, there are a number of differences in concept between the CPIH-consistent expenditure and Living Costs and Food (LCF), which mean that the data do not align closely in certain classes. This requires certain assumptions to overcome.
There is also a range of additional limitations that relate to the data sources used in this article, rather than the methods employed to calculate price indices and inflation rates.
First, while the LCF is a relatively large, continuous survey of household expenditure, it places a burden on respondents. Response rates have been declining over the last 10 years; response rates fell from 62% in 2001 to 48% in 2013. As there are no obvious candidate variables that could be used as exclusion restrictions, we have not been able to model this process of non-response. This may affect our results if non-reporting households have very different patterns of expenditure to those who do report, although non-response weighting is used throughout to alleviate this issue.
Analysis of the response rate suggests that some types of household are less likely to respond to the LCF, but without more detailed information it is difficult to assess the likely size or direction of this effect. Pooling the LCF data to increase the sample size was also considered but as the LCF data is weighted annually to reflect mid-year population estimates, pooling the data would require reweighting. The pooled dataset would also ideally be centred at y-2, which means that the dataset would not provide timely estimates of expenditure.
Secondly, the LCF only samples from UK private households. This means that it does not cover some types of household that might be of interest. In particular, it does not cover student halls and other communal establishments, for example, nursing homes.
5.3 Vintages of the LCF
To be consistent with the CPIH methodology, the LCF expenditure data has been taken from two years before the year for which the CPIH is calculated and then price updated (Section 4). This ensures that the expenditures measured in both sources cover the same period and minimise any mismatch that might occur. One problem is that the population characteristics might have changed in the interim so that the household groups observed in the LCF in year y-2 might be different to the current household groups. This has been checked for the expenditure deciles1 and the household type groups (retired households and households with and without children).
One of the difficulties with this analysis is that the LCF is a cross-sectional survey, which means that a household isn’t tracked over time. Therefore, it is difficult to analyse whether the characteristics change over time as a household won’t exist in two consecutive datasets, but we can look at this in aggregate. The approach used was to consider the 95% confidence interval of the y-2 weighted proportion and if the y-1 household groups were within this interval, then the conclusion was that the household groups were only differing by chance and not due to sample rotation. For most of the years, this is the case and therefore using the same year as the CPIH-consistent data is justified from a household group point of view as well as from an expenditure point of view.
Notes for: Limitations
- Income deciles show the same pattern as expenditure deciles for this analysis.
6. Annex A: Imputed rents methodology
This annex provides further information about the methodology used to construct imputed rents at the household level. It also contains details of the methodological improvements that have been implemented since the previous release in 2017.
In the previous release, all households not categorised as owner occupiers were considered “renters”. This included local authority tenants, housing association tenants , private tenants in both furnished and unfurnished properties, and those living “rent free”.
The Valuation Office Agency data currently used to impute rent in the Consumer Prices Index including owner occupiers’ housing costs (CPIH) is restricted to private tenancies that are not supported (either wholly or in part) by housing benefit. In addition, the CPIH Compendium states that “...furnished rentals are not appropriate for rental equivalence…”. Therefore, to maintain consistency with the CPIH, the definition of a “renter” for the purpose of this analysis has been changed to include only private, unfurnished, and unsubsidised tenancies; further references to “renters” or “rent” in this Annex relate specifically to these tenancies. Households with other rental tenancy types (local authority tenants, housing association tenants , private tenants in unfurnished properties, those living “rent free”, and any additional renters receiving housing benefit) have been removed from the data prior to modelling.
The use of a two-stage Heckman model accounts for any selection bias1 in the data. This is because the household characteristic of “Renting” doesn’t occur at random – people live in rented accommodation rather than owning their own home for a variety of reasons. For example, households with low income may be more likely to rent than own. Therefore, whether we observe their rent in our data is not random, so the sample of observed rent would be biased and it is not possible to use ordinary regression. This bias is known as selection bias, and if it isn’t accounted for then the model may not provide accurate estimates of the imputed rent for owner occupiers.
The two-stage Heckman model explains rent paid as a function of the characteristics of the house itself and the people living there, while also partially accounting for selection into rented accommodation. The Heckman model is also known as the Heckman correction as it aims to correct for the selection bias. The two stages of the model are as follows:
1. The selection equation – this estimates the probability of being a renter given certain characteristics, this is a probit regression:
2. The outcome equation – this estimates the level of rent based on characteristics and expenditure information, using a weighted least squares regression:
For the modelling, two separate models were estimated: one for Great Britain (England, Scotland and Wales) and another for Northern Ireland. This is because some of the variables are collected differently in Northern Ireland.
There are three stages in our estimation of imputed rent:
1. estimate the coefficients in the selection equation and compute the bias correction
2. estimate the level of rent using the outcome equation
3. calibrate these data with higher level Valuation Office Agency averages
For the first two steps the data is pooled over all of the years of analysis. This improves the sample sizes, particularly for Northern Ireland.
Stage 1 – Selection equation
A household is defined as a renter using the tenure type variable and the housing benefit variable (as described above) on the Living Costs and Food (LCF) survey.
The selection equation for the Great Britain data was estimated with the following form:
Equation A.1
For the Northern Ireland data, the same model was used but the Region variable was removed.
Models were selected based on the lowest Akaike Information Criterion (AIC)2. This means that the models have a good fit and are preferred to models with more explanatory variables.
As an example, Table 1 contains information for a fictitious household. Using this information and the selection equation [A.1], the probability of that household being a renter is:
This means that the probability of this household being a renter is 2%.
Table 1: Characteristics and expenditures for a fictitious household
| Variable | Value |
|---|---|
| Year | 2015 |
| Housing type | Semi-detached house |
| Region | Wales |
| Number of adults | 2 |
| Number of children | 3 |
| Percentile of total expenditure | 80 |
| Number of rooms | 8 |
| Socioeconomic group | Higher professional – employee |
| Expenditure on repairs | £5 |
| Expenditure on pets | £10 |
| Council Tax band | C |
| Housing Benefit | £0.50 |
| Expenditure on education | £0 |
| Expenditure on housing, water, and electricity | £20 |
| Source: Office for National Statistics | |
| Notes: | |
| 1. Expenditures and housing benefit are given in £ per week. | |
Download this table Table 1: Characteristics and expenditures for a fictitious household
.xls (27.6 kB)Once this probability is calculated, the selection bias correction can then be estimated. This correction in the Heckman model is called the inverse Mills ratio (IMR), defined as:
Equation A.2
For our example household in Table 1, the IMR is 2.45.
The IMR is used in the next stage of the methodology.
Stage 2 – Outcome equation
The next stage is to estimate the level of rent an owner occupier would be paying if they rented their own home. This is done by building the model on those in the LCF dataset that are renters and estimating the coefficients of the outcome equation.
The distribution of rent is positively skewed; therefore a transformation of the rent variable is required to overcome this. This makes it easier to model rent using regression techniques. The transformation used is in the Box-Cox family of transformations defined in equation [A.3], using y as the response variable:
Equation A.3
This has the advantage of stabilising the variance and making the distribution closer to the normal distribution. The value of λ was chosen, which maximised the profile log-likelihood. For the Great Britain model, λ=0.6 maximises the profile log-likelihood and for Northern Ireland, λ=1.53 does. The transformation as a by-product meant that the model diagnostics improved compared with what they were before the transformation.
Before the models were fitted, households that had weekly rents that were less than £5 or greater than £500 were removed from the dataset for Great Britain and greater than £150 for Northern Ireland data. These households make up around 2% of the dataset and there isn’t enough information to accurately predict the level of rent for these households. This means that they could impact on the accuracy of prediction by influencing the estimates of the coefficients.
The following model was used to estimate rent:
Equation A.4
Previously, a weighted least squares (WLS) regression was used, with the annual LCF-calibrated survey weight used as the weight in the model. This resulted in a high model variance, which in turn caused the bias correction applied during the Box-Cox back-transformation to produce nonsensical results.
In addition , it was determined that since the purpose of this model is to predict values for a given dataset (sample), rather than to provide estimates and inferences of parameters intended to be representative of the whole LCF population, it was not conceptually necessary to use a WLS regression. Therefore, the imputed rent estimates are now produced using an ordinary least squares (OLS) regression model.
The model includes the inverse Mills ratio (IMR) as an additional explanatory variable to account for the selection bias.
For the Northern Ireland data, the same model was used but the Council Tax band variable was removed. The equivalent of Council Tax in Northern Ireland is rates, but this is not banded as it is in Great Britain and therefore it isn’t included in the model for Northern Ireland.
In the previous release, the model also included a variable relating to council tax rebate or allowance. This variable is used to calculate the value of rent (the dependent variable in the model) and is therefore unsuitable for use as an independent variable in the model.
The models were estimated and households with high studentised residuals3 were removed. The models were then re-estimated. This removed a small number of the households but improved the model diagnostics.
These models were then used to estimate the Box-Cox transformed rent for owner occupiers identified in the LCF data and then transformed back to rent on the original scale. The reverse transformation formula has been amended to include a bias correction term, in order to account for bias that is inherent when back-transforming predictions made on a Box-Cox transformed variable. The rent values are calculated using the model output predictions according to the following formula:
Equation A.5
For example, the fictitious owner occupier household in Table 1 has a predicted value of transformed rent equal to:
The inverse Box-Cox transformation is then applied, giving the household’s predicted rent equal to £28.11 a week.
Stage 3 – Calibration
The final step is to calibrate the data to the VOA higher-level estimates. This is to ensure that the estimated levels of expenditure closely match the ones used in the CPIH aggregate measure. The VOA data also have a larger sample size than the LCF data.
The VOA data include information on the average monthly rent by year for each region. These are converted into weekly values for consistency with the LCF data. The imputed rents estimates calculated in Stage 2 are then calibrated using the following formula:
Notes for: Annex A – Imputed rents methodology
Selection bias is the bias introduced by the selection of individuals, groups or data for analysis in such a way that proper randomisation is not achieved, thereby ensuring that the sample obtained is not representative of the population intended to be analysed.
The AIC is a measure of relative quality of a statistical model, it measures the information lost when using a model. The better the model is, the smaller the value of the AIC.
A studentised residual is a residual divided by its standard error, that is:
7. Annex B: Imputed rents distribution on a regional and country basis
Figure 3 is analogous to Figure 2 shown in Section 4, but on a regional and country basis rather than a national one. This demonstrates the impact of including a region variable in the model and also shows the effect of the calibration stage.
As at the national level, average calibrated imputed rent is slightly greater than average actual rent for each of the regions. As expected, the average imputed rent for London is greater than that for the other regions, however, there also appears to be relatively high variance in the London distribution, which might be due to the composition of the housing stock in the different areas of London.
Northern regions such as the North West, North East, and Yorkshire and The Humber show a lower expenditure for both rent and imputed rent than some of the southern regions such as the South East, South West and East of England regions. The distribution of imputed rent in Wales is bimodal, which may reflect differences between rural and urban areas in Wales.
Figure 3: Distribution of actual rent and imputed rent on a Living Costs and Food Survey and Valuation Office Agency basis, by region and country
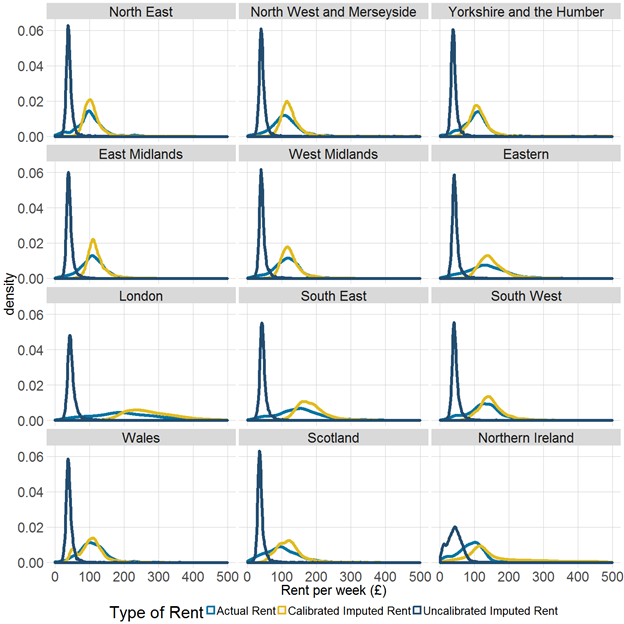
Source: Office for National Statistics
Notes:
- These charts are based on the underlying distribution of the data. The line is a continuous function (that is, it is created using a model to estimate the equation of the plotted line) and therefore there are no underlying data values that can be downloaded.
Download this image Figure 3: Distribution of actual rent and imputed rent on a Living Costs and Food Survey and Valuation Office Agency basis, by region and country
.png (127.8 kB)9. Acknowledgements
The authors would like to thank the contributions of Rob Bucknall of Methodology and Chris Payne, Onyinye Ezeyi, Helen Sands, Arturas Eidukas and Andreas Soteriades of Prices Division.
Nôl i'r tabl cynnwys